Условие гармонических колебаний. Гармонические колебания (уравнение, характеристика, график). Уравнение состояния идеального газа

В повседневной жизни и в технике мы постоянно сталкиваемся с колебательным движением: маятник стенных часов совершает периодические качания около отвесного положения, кузов автомашины или вагона качается на мягких рессорах и т. д. Во многих случаях различным колебательным движениям присущ общий признак, заключающийся в существовании некоторого устойчивого положения, в котором колеблющееся тело пребывает до и после колебаний и в котором оно может находиться неопределенно долгое время - до тех пор, пока внешняя сила не выведет его из этого устойчивого состояния. Для маятника таким устойчивым положением является отвесное; для фундамента машины и подвешенного на рессорах вагона - положение, соответствующее некоторой постоянной деформации, обусловленной весом машины или вагона.

Всегда, когда выводят тело из устойчивого положения, возникает сила, стремящаяся возвратить тело в начальное положение. Происхождение этой силы может быть различным. Для маятника - это сила тяжести, для кузова вагона - упругость рессор.

Наличие возвращающей силы является еще недостаточным условием возникновения колебательного движения. В колебательном движении, помимо возвращающей силы, должен участвовать еще и другой фактор, не позволяющий колеблющемуся телу сразу же остановиться в той точке его пути, которая соответствует устойчивому состоянию. Этим фактором является инерция колеблющегося тела.

Колебательное движение имеет особенно простой характер в том случае, когда возвращающаяся сила возрастает пропорционально смещению колеблющегося тела из положения равновесия. Сначала мы рассмотрим этот случай чисто кинематически.

Представим себе точку (рис. 126), движущуюся по кругу радиуса а с постоянной угловой скоростью и рассмотрим движение проекции этой точки на вертикальную ось. Пусть в момент

времени радиус повернулся из начального положения на угол тогда смещение х точки равное отрезку определяется простым выражением:

Угол называют фазой колебания точки зная угловую скорость

(где время обхода точкой полной окружности, а длина дуги полной окружности в угловых единицах), нетрудно найти фазу

и, следовательно,

Рис. 126. При равномерном движении точки по кругу ее проекция совершает гармоническое колебание.

Рассматривая движение проекции точки на горизонтальную ось, аналогично получаем:

Колебательный характер движения, выражаемого уравнениями (1) и становится особенно очевидным, когда они представлены, как это сделано на рис. 127, графически

Рис. 127. а - амплитуда гармонического колебания, период.

Колебательное движение, выражаемое функцией синуса или косинуса, называют простым гармоническим колебанием; оно полностью характеризуется следующими величинами:

1. Расстоянием (а) наибольшего отклонения от начального положения - амплитудой.

2. Периодом колебания т. е. временем, в течение которого колеблющаяся точка (или тело) совершает полный цикл колебательного движения, смещаясь сначала в одну, а затем в другую сторону от начального положения и снова возвращаясь к нему.

Вместо периода колебания можно задать его частоту определяемую числом полных колебаний, совершаемых в течение 1 сек. Единицу частоты - одно колебание в называют герц. Очевидно, что период и частота являются относительно друг друга обратными величинами:

Угловая частота о однозначно определяется периодом или частотой:

Очевидно, что со означает число полных колебаний, совершаемых в течение секунд.

Перейдем к рассмотрению сил, под действием которых может возникнуть простое гармоническое колебание. Для этого, воспользовавшись уравнением (1), найдем сначала скорость и ускорение гармонически колеблющейся точки:

Последнее выражение означает, что в каждый данный момент времени ускорение пропорционально смещению х точки из начального положения; знак минус указывает, что ускорение всегда направлено противоположно смещению. Ускорение пропорционально вызывающей его силе и направлено в ту же сторону, что и сила; значит, сила, обусловливающая ускорение колеблющегося тела, направлена тоже в сторону, противоположную смещению, и пропорциональна величине смещения. Очевидно, что эта сила и есть сила, возвращающая точку к положению равновесия.

Умножая обе части уравнения (5) на массу колеблющейся материальной точки, мы получим дифференциальное уравнение простого гармонического колебания:

Уравнение (6) имеет простой физический смысл: в левой его части стоит произведение массы колеблющейся точки на ее ускорение, чем и определяется согласно второму закону Ньютона действующая на точку возвращающая сила - Таким образом, уравнение (6) выражает второй закон механики применительно к

случаю материальной точки, связанной с положением равновесия силой, пропорциональной смещению. Обратно, при наличии возвращающей силы, пропорциональной смещению тела, последнее будет совершать простое гармоническое колебание, выражаемое уравнениями (1) или

Теория гармонических колебаний играет в физике совершенно исключительную по своему значению роль. Учение о гармонических колебаниях используется во всех отделах физики: в теории упругости, в акустике, в оптике, в учении об электричестве, в кинетической теории материи, в теории атома. Чем объясняется эта универсальная применимость учения о гармонических колебаниях?

Исключительная роль учения о гармонических колебаниях объясняется двумя обстоятельствами. Гармоническое колебание - это движение, вызванное силой, возрастающей пропорционально отклонению х от положения равновесия. Какова бы ни была в действительности зависимость силы от зависимость эта всегда может быть представлена в виде бесконечного ряда Тейлора; первым членом этого ряда является квазиупругая сила (т. е. сила, пропорциональная остальные члены ряда пропорциональны последовательно возрастающим степеням Если смещение мало, старшими членами ряда можно пренебречь, - это случай гармонического колебания. При значительных отклонениях от положения равновесия нужно учитывать второй, третий и другие члены ряда (в этом случае. колебания ангармоничны). По мере роста амплитуды колебательное движение обычно все более и более уклоняется от гармонического колебания. Но и в этом случае каждый раз, когда колеблющаяся система подходит к положению равновесия, поочередно отпадает влияние старших членов ряда Тейлора и близ положения равновесия движение определяется уже одной квазиупругой силой. Поэтому теория гармонических колебательных движений является первым и неизбежным шагом на пути к исследованию почти всех периодических процессов.

Второе обстоятельство, делающее теорию гармонических колебаний весьма важной для различных отделов физики, заключается в том, что многие колебательные системы при внешнем периодическом воздействии на них «отзываются» (резонируют) на гармонические колебания, частота которых близка к частоте собственных колебаний системы (§ 61).

Федун В.И. Конспект лекций по физике Механические колебания и волны

Колебания и упругие волны.

Лекция 9.

8 . Гармонические колебания и их основные характеристики.

8. 1. Свободные колебания и их основные характеристтики. Представления гармонических колебаний.

Колебательным движением называется движение, обладающее той или иной степенью повторяемости во времени. Движение называется периодическим , если значения величин, изменяющихся в процессе движения. Повторяются через равные промежутки времени.

Систему, совершающую колебания, независимо от ее природы называют осциллятором .

Свободные колебания. Для тела (точки), совершающей колебания, существует положение устойчивого равновесия. Вывести тело из этого состояния можно, приложив внешнюю силу. Тело, выведенное из состояния равновесия и представленное самому себе, совершает колебания около положения равновесия. Такие колебания называются собственными или свободными . Частота , с которой система совершает такие колебания, называется собственной.

Аналитическое представление гармонических колебаний не менее известно:

где - колеблющаяся величина (смещение, скорость, ускорение, сила и т.п.), - время, - амплитуда колебания (амплитуда равна максимальному абсолютному значению отклонения колеблющейся величины от положения равновесия), - циклическая или круговая частота.

Физический смысл циклической частоты состоит в том, что она численно равна числу колебаний, совершаемых за
секунд, т.е.

где - частота колебаний, т.е. число колебаний, совершаемых за единицу времени, - период колебаний – время, за которое совершается одно полное колебание.

Величина
называется фазой колебания. Фаза колебания – функция времени, которая определяет значение колеблющейся величины в данный момент времени . Она показывает, какую часть от амплитуды составляет смещение в данный момент времени:
. Величина называется начальной фазой колебания. Она определяет значение величины в начальный момент времени
.

Наконец, в векторном представлении колебание представляется в виде вектора, длина которого пропорциональна амплитуде колебаний (см. рис.8.2). Сам вектор вращается в плоскости чертежа с угловой скоростью  вокруг оси, перпендикулярной этой плоскости и проходящей через начало вектора

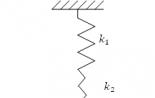
8. 2. Пружинный маятник. Дифференциальное уравнение свободных колебаний.

Пружинный маятник . Примером гармонического осциллятора является пружинный маятник. Пружинный маятник – это груз массой т , закрепленный на абсолютно упругой пружине (см. рис. 8.3) и совершающий гармонические колебания под действием упругой или квазиупругой силы (силы, имеющие иную природу, чем упругие силы, но также

Такая сила называется возвращающей силой. По второму закону Ньютона для возвращающей силы имеем

получаем дифференциальное уравнение собственных колебаний

или после перехода от комплексной формы к тригонометрической

8. 3. 1. Физический маятник.

Рассмотрим вращение массивного тела (см. рис.8.4) вокруг неподвижной оси при малых отклонениях этого тела от положения равновесия. В этом случае такое тело называют физическим маятником . Уравнением движение этого тела является основное уравнение динамики вращательного движения

где - момент инерции тела, вычисленный относительно оси вращения,
- главный вектор моментов сил, - угол поворота тела,
- угловое ускорение тела.

Напомним, что является псевдовектором, который направлен вдоль оси вращения и подчиняется правилу правого винта. Поэтому на рис. 8.4 вектор направлен за плоскость рисунка.

К вращению тело приводит только момент силы тяжести
, точка приложения которой совпадает с центром инерции тела. Поэтому главный вектор моментов сил

где
- расстояние от оси вращения до центра инерции,
-масса тела

Проектируя (9) на ось вращения получаем дифференциальное уравнение колебаний физического маятника

8. 3. 2. Математический маятник.

Если размеры тела много меньше расстояния от оси вращения до центра инерции, то физический маятник можно считать математическим . Здесь проверим справедливость этого утверждения сделав предельный переход для частоты колебаний, определяемой по (8.13).

По теореме Штейнера момент инерции
, - момент инерции относительно оси, проходящей через центр инерции. Если достаточно велико, то
. Следовательно,

8. 4. Скорость и ускорение тела, участвующего в гармонических колебаниях. Кинетическая, потенциальная и полная механическая энергия осциллятора.

На примере пружинного маятника найдем скорость и ускорение тела, совершающего колебательное движение. По определению скорость тела
. Следовательно, при гармонических колебаниях согласно (8.1)

Тогда по основному закону динамики возвращающая сила

Потенциальная энергия деформированной пружины

Уравнение гармонического колебания

Уравнение гармонического колебания устанавливает зависимость координаты тела от времени

График косинуса в начальный момент имеет максимальное значение, а график синуса имеет в начальный момент нулевое значение. Если колебание начинаем исследовать из положения равновесия, то колебание будет повторять синусоиду. Если колебание начинаем рассматривать из положения максимального отклонения, то колебание опишет косинус. Или такое колебание можно описать формулой синуса с начальной фазой .

Изменение скорости и ускорения при гармоническом колебании

Не только координата тела изменяется со временем по закону синуса или косинуса. Но и такие величины, как сила , скорость и ускорение , тоже изменяются аналогично. Сила и ускорение максимальные, когда колеблющееся тело находится в крайних положениях, где смещение максимально, и равны нулю, когда тело проходит через положение равновесия. Скорость, наоборот, в крайних положениях равна нулю, а при прохождении телом положения равновесия - достигает максимального значения.

Если колебание описывать по закону косинуса

Если колебание описывать по закону синуса

Максимальные значения скорости и ускорения

Проанализировав уравнения зависимости v(t) и a(t), можно догадаться, что максимальные значения скорость и ускорение принимают в том случае, когда тригонометрический множитель равен 1 или -1. Определяются по формуле

Движение маятника в часах, землетрясение, переменный ток в электрической цепи, процессы радиопередачи и радиоприема - это совершенно различные, не связанные друг с другом процессы. Каждый из них имеет свои особые причины, но их объединяет один признак - признак общности характера изменения физических величин с течением времени. Эти и многие другие процессы различной физической природы во многих случаях оказывается целесообразным рассматривать как один особый тип физических явлений - колебания.

Общий признак физических явлений, называемых колебаниями, - это их повторяемость во времени. При различной физической природе многие колебания происходят по одинаковым законам, что позволяет применять общие методы для их описания и анализа.

Гармонические колебания. Из большого числа различных колебаний в природе и технике особенно часто встречаются гармонические колебания. Гармоническими называют колебания, совершающиеся по закону косинуса или синуса:

где - величина, испытывающая колебания; - время; - постоянная величина, смысл которой будет выяснен далее.

Максимальное значение величины, изменяющейся по гармоническому закону, называют амплитудой колебаний. Аргумент косинуса или синуса при гармонических колебаниях называют фазой колебания

Фазу колебания в начальный момент времени называют начальной фазой. Начальная фаза определяет значение величины в начальный момент времени

Значения функции синуса или косинуса при изменении аргумента функции на повторяются, поэтому при гармонических колебаниях значения величины повторяются при изменении фазы колебания на . С другой стороны, при гармоническом колебании величина должна принимать те же значения через интервал времени, называемый периодом колебаний Т. Следовательно, изменение фазы на происходит

через период колебаний Т. Для случая, когда получим:

Из выражения (1.2) следует, что постоянная в уравнении гармонических колебаний есть число колебаний, происходящих за секунд. Величину называют циклической частотой колебаний. Используя выражение (1.2), уравнение (1.1) можно выразить через частоту или период Т колебаний:

Наряду с аналитическим способом описания гармонических колебаний широко используют графические способы их представления.

Первый способ - задание графика колебаний в декартовой системе координат. По оси абсцисс откладывают время I, а по оси ординат - значение изменяющейся величины Для гармонических колебаний этот график - синусоида или косинусоида (рис. 1).

Второй способ представления колебательного процесса - спектральный. По оси ординат отсчитывают амплитуду, а по оси абсцисс - частоту гармонических колебаний. Гармонический колебательный процесс с частотой и амплитудой представлен в этом случае вертикальным отрезком прямой длиной проведенным от точки с координатой на оси абсцисс (рис. 2).

Третий способ описания гармонических колебаний - метод векторных диаграмм. В этом способе используют следующий, чисто формальный прием для нахождения в любой момент времени значения величины изменяющейся по гармоническому закону:

Выберем на плоскости произвольно направленную координатную ось по которой будем отсчитывать интересующую нас величину Из начала координат вдоль оси проведем вектор модуль которого равен амплитуде гармонического колебания хт. Если теперь представим себе, что вектор вращается вокруг начала координат в плоскости с постоянной угловой скоростью со против часовой стрелки, то угол а между вращающимся вектором и осью в любой момент времени определится выражением.