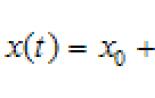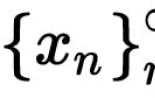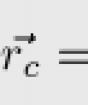Ano ang sentro ng masa ng katawan. Sentro ng misa. Solid figure center ng masa

Sentro ng grabidad(o sentro ng misa) ng isang katawan ay tinatawag na isang punto na mayroong pag-aari na kung ang katawan ay nasuspinde mula sa puntong ito, mananatili ang posisyon nito.

Sa ibaba ay isinasaalang-alang namin ang mga dalawang-dimensional at tatlong-dimensional na mga problema na nauugnay sa paghahanap para sa iba't ibang mga sentro ng masa - pangunahin mula sa pananaw ng computational geometry.

Ang mga solusyon na isinasaalang-alang sa ibaba ay maaaring nahahati sa dalawang pangunahing katotohanan... Ang una ay ang gitna ng masa ng isang sistema ng mga materyal na puntos na katumbas ng average ng kanilang mga coordinate, na kinunan ng mga coefficients na proporsyonal sa kanilang masa. Ang pangalawang katotohanan ay kung alam natin ang mga sentro ng masa ng dalawang hindi nag-intersect na numero, kung gayon ang sentro ng masa ng kanilang unyon ay mahiga sa segment na kumukonekta sa dalawang sentro na ito, at hahatiin ito sa parehong ratio tulad ng masa ng ang pangalawang pigura ay nauugnay sa masa ng una.

Kaso ng 2D: mga polygon

Sa katunayan, kapag pinag-uusapan ang tungkol sa gitna ng masa ng isang dalawang-dimensional na pigura, ang isa ay maaaring mangahulugan ng isa sa mga sumusunod na tatlo gawain:

• Ang gitna ng masa ng point system - ibig sabihin ang lahat ng masa ay nakatuon lamang sa mga vertex ng polygon.
• Ang gitna ng gravity ng frame - ibig sabihin ang masa ng polygon ay nakatuon sa perimeter nito.
• Ang gitna ng masa ng isang solidong pigura - ibig sabihin ang masa ng isang polygon ay ipinamamahagi sa buong lugar nito.

Ang bawat isa sa mga gawaing ito ay may isang malayang solusyon, at isasaalang-alang nang magkahiwalay sa ibaba.

Center ng masa ng point system

Ito ang pinakasimpleng ng tatlong mga problema, at ang solusyon nito ay ang kilalang pisikal na pormula ng gitna ng masa ng isang sistema ng mga materyal na puntos:

kung saan ang mga masa ng mga puntos, ay ang kanilang mga radius vector (na tumutukoy sa kanilang posisyon na may kaugnayan sa pinagmulan), at ang kinakailangang radius vector ng gitna ng masa.

Sa partikular, kung ang lahat ng mga puntos ay may parehong masa, kung gayon ang mga coordinate ng gitna ng masa ay average mga coordinate ng mga puntos. Para kay tatsulok ang puntong ito ay tinawag centroid at kasabay ng punto ng intersection ng mga median:

Para kay patunay ng ng mga pormulang ito, sapat na upang matandaan na ang balanse ay nakakamit sa isang punto kung saan ang kabuuan ng mga sandali ng lahat ng mga puwersa ay katumbas ng zero. Sa kasong ito, ito ay nagiging isang kundisyon na ang kabuuan ng mga radius vector ng lahat ng mga puntos na may kaugnayan sa punto, na pinarami ng mga masa ng mga kaukulang puntos, ay katumbas ng zero:

at, na nagpapahayag mula dito, nakukuha namin ang kinakailangang formula.

Center ng gravity ng frame

Ngunit pagkatapos ang bawat panig ng polygon ay maaaring mapalitan ng isang punto - ang gitna ng segment na ito (dahil ang gitna ng masa ng isang homogenous na segment ay ang gitna ng segment na ito), na may isang mass na katumbas ng haba ng segment na ito.

Ngayon nakuha namin ang problema tungkol sa sistema ng mga materyal na puntos, at inilalapat ang solusyon mula sa nakaraang talata dito, nakita namin:

kung saan ang midpoint ng -th na bahagi ng polygon, ay ang haba ng -th na bahagi, ay ang perimeter, ibig sabihin ang kabuuan ng haba ng mga gilid.

Para kay tatsulok maaaring ipakita ang sumusunod na pahayag: ang puntong ito ay intersection point ng mga bisector isang tatsulok na nabuo ng mga midpoints ng mga gilid ng orihinal na tatsulok. (upang maipakita ito, kailangan mong gamitin ang pormula sa itaas, at pagkatapos ay mapansin na hinati ng mga bisector ang mga gilid ng nagresultang tatsulok sa parehong sukat bilang mga sentro ng masa ng mga panig na ito).

Solid figure center ng masa

Ipinapalagay namin na ang masa ay pantay na ipinamamahagi sa pigura, ibig sabihin ang density sa bawat punto ng figure ay katumbas ng parehong numero.

Kaso ng tatsulok

Nagtalo na para sa isang tatsulok, ang sagot ay magiging pareho centroid, ibig sabihin ang puntong nabuo ng arithmetic mean ng mga coordinate ng mga vertex:

Kaso ng tatsulok: patunay

Narito ang isang patunay sa elementarya na hindi gumagamit ng teorya ng mga integral.

Ang Archimedes ay ang unang nagbigay ng tulad ng isang pulos geometric na patunay, ngunit ito ay napaka-kumplikado, na may isang malaking bilang ng mga geometric konstruksyon. Ang ebidensyang ipinakita dito ay mula sa Apostol, artikulo ni Mnatsakanian na "Paghahanap ng Mga Centroid na Madaling Daan".

Ang patunay na halaga sa pagpapakita na ang gitna ng masa ng tatsulok ay nakasalalay sa isa sa mga median; na inuulit ang prosesong ito nang dalawang beses pa, ipapakita namin sa gayon na ang gitna ng masa ay nakasalalay sa punto ng intersection ng mga median, na kung saan ay ang centroid.

Hatiin namin ang tatsulok na ito sa apat, na kumokonekta sa mga midpoint ng mga gilid, tulad ng ipinakita sa pigura:

Ang apat na nagresultang mga triangles ay tulad ng isang coefficient triangle.

Ang mga Triangles No. 1 at No. 2 ay magkasama na bumubuo ng isang parallelogram, ang gitna ng masa na kung saan ay nakasalalay sa punto ng intersection ng mga diagonals nito (dahil ito ay isang figure na simetriko tungkol sa parehong diagonals, na nangangahulugang ang gitna ng masa ay dapat na nakasalalay sa bawat isa ng dalawang diagonals). Ang punto ay nasa gitna ng karaniwang bahagi ng mga tatsulok na Blg. 1 at Blg. 2, at nakasalalay din sa panggitna ng tatsulok:

Hayaan ngayon ang vector ay isang vector na iginuhit mula sa vertex hanggang sa gitna ng masa ng tatsulok na Blg. 1, at hayaang ang vector ay isang vector na iginuhit mula sa puntong (kung saan, alalahanin, ay ang gitna ng gilid kung saan ito namamalagi) :

Ang aming layunin ay upang ipakita ang mga vector at collinear.

Ipaalam natin sa pamamagitan ng at ang mga puntos na sentro ng masa ng mga triangles Blg. 3 at Blg. 4. Pagkatapos, malinaw naman, ang gitna ng masa ng hanay ng dalawang triangles na ito ang magiging puntong iyon na ang midpoint ng segment. Bukod dito, ang vector mula sa bawat punto ay pareho ng vector.

Ang nais na gitna ng masa ng tatsulok ay nakasalalay sa gitna ng segment na kumukonekta sa mga puntos at (dahil hinati namin ang tatsulok sa dalawang bahagi ng pantay na mga lugar: Hindi. 1-Hindi. 2 at Hindi. 3-Hindi. 4):

Kaya, ang vector mula sa vertex hanggang sa centroid ay. Sa kabilang banda, mula pa ang tatsulok # 1 ay katulad ng isang tatsulok na may isang coefficient, pagkatapos ay ang parehong vector ay. Mula dito nakukuha natin ang equation:

kung saan namin mahahanap:

Sa gayon, napatunayan namin na ang mga vector at collinear, na nangangahulugang ang nais na centroid ay nakasalalay sa panggitna na papalabas mula sa kaitaasan.

Bukod dito, kasama ang paraan, pinatunayan namin na ang centroid ay naghahati sa bawat panggitna na may kaugnayan, pagbibilang mula sa itaas.

Kaso ng polygon

Ngayon lumipat tayo sa pangkalahatang kaso - i. sa okasyon polygon... Para sa kanya, ang gayong pangangatuwiran ay hindi na naaangkop, kaya binabawas natin ang problema sa isang tatsulok: samakatuwid, hinahati namin ang polygon sa mga tatsulok (ibig sabihin, tatsulokin ito), hanapin ang gitna ng masa ng bawat tatsulok, at pagkatapos ay hanapin ang gitna ng masa ng mga nagresultang sentro ng masa ng mga triangles.

Ang pangwakas na pormula ay ang mga sumusunod:

kung saan ang centroid ng tatsulok na ika sa tatsulok ng isang naibigay na polygon, ay ang lugar ng tatsulok na tatsulok, ay ang lugar ng buong polygon.

Ang pag-triangulate ng isang convex polygon ay isang walang halaga na gawain: para dito, halimbawa, maaari kang kumuha ng mga triangles, kung saan.

Kaso ng polygon: alternatibong paraan

Sa kabilang banda, ang aplikasyon ng formula sa itaas ay hindi masyadong maginhawa para sa mga non-convex polygon sapagkat ang pag-triangulate sa kanila ay hindi isang madaling gawain. Ngunit para sa mga naturang polygon, maaari kang mag-isip ng isang mas simpleng diskarte. Sa gayon, gumuhit tayo ng isang pagkakatulad sa kung paano mo mahahanap ang lugar ng isang di-makatwirang polygon: isang arbitraryong punto ang napili, at pagkatapos ay ang mga lugar ng pag-sign ng mga triangles na nabuo ng puntong ito at ang mga puntos ng polygon ay na-buod:. Ang isang katulad na pamamaraan ay maaaring mailapat upang mahanap ang gitna ng masa: ngayon lamang namin ibubu-buo ang mga sentro ng masa ng mga triangles na kinuha kasama ang mga coefficients na proporsyonal sa kanilang mga lugar, ibig sabihin. ang pangwakas na pormula para sa gitna ng masa ay:

kung saan ay isang arbitrary point, ay ang mga puntos ng polygon, ay ang centroid ng tatsulok, ay ang sign area ng tatsulok na ito, ay ang sign area ng buong polygon (ibig sabihin).

Tatlong-dimensional na kaso: polyhedra

Katulad ng kaso ng dalawang-dimensional, sa 3D maaaring magsalita ang isa tungkol sa apat na posibleng mga pahayag sa problema nang sabay-sabay:

• Ang gitna ng masa ng sistema ng mga puntos - ang mga vertex ng polyhedron.
• Ang gitna ng masa ng frame ay ang mga gilid ng polyhedron.
• Ang gitna ng masa ng ibabaw - ibig sabihin ang masa ay ipinamamahagi sa ibabaw ng lugar ng polyhedron.
• Ang gitna ng masa ng isang solidong polyhedron - ibig sabihin ang masa ay ipinamamahagi sa buong polyhedron.

Center ng masa ng point system

Tulad ng sa 2D na kaso, maaari kaming mag-apply ng isang pisikal na pormula at makuha ang parehong resulta:

na, sa kaso ng pantay na masa, nagiging arithmetic mean ng mga coordinate ng lahat ng mga puntos.

Sentro ng gravity ng frame ng polyhedron

Katulad ng kaso ng dalawang-dimensional, pinapalitan lamang namin ang bawat gilid ng polyhedron ng isang materyal na punto na matatagpuan sa gitna ng gilid na ito, at may isang masa na katumbas ng haba ng gilid na ito. Natanggap ang problema ng mga materyal na puntos, madali naming mahahanap ang solusyon nito bilang isang timbang na kabuuan ng mga coordinate ng mga puntong ito.

Center ng masa ng ibabaw ng isang polyhedron

Ang bawat mukha sa ibabaw ng isang polyhedron ay isang dalawang-dimensional na pigura, ang gitna ng masa na maaari nating hanapin. Natagpuan ang mga sentro ng masa at pinapalitan ang bawat mukha ng sentro ng masa, nagkakaroon kami ng problema sa mga materyal na puntos, na madaling lutasin.

Sentro ng masa ng isang solidong polyhedron

Kaso ng Tetrahedron

Tulad ng sa dalawang-dimensional na kaso, malutas muna natin ang pinakasimpleng problema - ang problema para sa isang tetrahedron.

Pinagtalunan na ang gitna ng masa ng isang tetrahedron ay kasabay ng punto ng intersection ng mga median nito (ang median ng isang tetrahedron ay isang segment na iginuhit mula sa tuktok nito patungo sa gitna ng masa ng tapat na mukha; kaya, ang median ng isang tetrahedron dumadaan sa tuktok at sa pamamagitan ng punto ng intersection ng mga medians ng isang tatsulok na mukha).

Bakit ganito? Dito, ang pangangatuwiran ay katulad ng dalawang-dimensional na kaso: kung pinutol namin ang tetrahedron sa dalawang tetrahedra gamit ang isang eroplano na dumadaan sa tuktok ng tetrahedron at ilang median ng kabaligtaran ng mukha, kung gayon ang parehong nagresultang tetrahedrons ay magkakaroon ng parehong dami (mula noong ang tatsulok na mukha ay nahahati ng median sa dalawang tatsulok na pantay na lugar, at ang taas ng dalawang tetrahedron ay hindi magbabago). Ang pag-uulit ng pangangatwirang ito ng maraming beses, nalaman namin na ang gitna ng masa ay nakasalalay sa punto ng intersection ng mga median ng tetrahedron.

Ang puntong ito - ang punto ng intersection ng mga median ng tetrahedron - ay tinawag na ito centroid... Maipapakita na talaga itong mayroong mga coordinate na katumbas ng arithmetic mean ng mga coordinate ng tetrahedron vertex:

(maaari itong maibawas mula sa katotohanang hinahati ng centroid ang mga median sa ratio)

Samakatuwid, walang pangunahing pagkakaiba sa pagitan ng mga kaso ng isang tetrahedron at isang tatsulok: isang punto na katumbas ng arithmetic na ibig sabihin ng mga vertex ay ang sentro ng masa sa dalawang pahayag ng problema nang sabay-sabay: kung ang mga masa ay matatagpuan lamang sa mga vertex , at kapag ang masa ay ipinamamahagi sa buong lugar / dami. Sa katunayan, ang resulta na ito ay pangkalahatan sa isang di-makatwirang sukat: ang gitna ng masa ng isang arbitrary simplex Ang (simplex) ay ang ibig sabihin ng arithmetic ng mga coordinate ng mga vertex nito.

Ang kaso ng isang di-makatwirang polytope

Bumabaling kami ngayon sa pangkalahatang kaso - ang kaso ng isang di-makatwirang polyhedron.

Muli, tulad ng sa dalawang-dimensional na kaso, binabawasan namin ang problemang ito sa isa na nalutas: hinati namin ang polyhedron sa tetrahedra (ibig sabihin, ginagawa namin ang tetrahedronization nito), hanapin ang gitna ng masa ng bawat isa sa kanila, at makuha ang pangwakas na sagot sa problema sa anyo ng isang bigat na kabuuan ng mga nahanap na sentro ng masa.

Sentro ng misa

gitna ng pagkawalang-galaw, isang punto ng geometriko, ang posisyon na kung saan ay nagpapakilala sa pamamahagi ng masa sa isang katawan o mekanikal na sistema. Ang mga coordinate ng Ts.m. ay natutukoy ng mga formula

,

kung saan m sa - masa ng mga materyal na puntos na bumubuo ng isang system, x k, y k, z k - mga coordinate ng mga puntong ito, M= Σ m sa - ang dami ng system, ρ ang density, V - dami Ang konsepto ng isang sentro ng grabidad ay naiiba sa konsepto ng isang sentro ng grabidad (tingnan ang Sentro ng grabidad) na ang huli ay may katuturan lamang para sa isang solidong katawan sa isang pare-parehong larangan ng grabidad; ang konsepto ng isang sentralisadong metal ay hindi nauugnay sa anumang lakas ng patlang at may katuturan para sa anumang mekanikal na sistema. Para sa isang matibay na katawan, magkatugma ang mga posisyon ng gitnang katawan at ang gitna ng grabidad.

Kapag lumipat ang isang sistemang mekanikal, ang CM nito ay gumagalaw sa parehong paraan tulad ng isang materyal na punto na gumagalaw, na mayroong isang masa na katumbas ng masa ng system at nasa ilalim ng impluwensya ng lahat ng mga panlabas na pwersa na inilapat sa system. Bilang karagdagan, ang ilang mga equation ng paggalaw ng isang mekanikal na sistema (katawan) na may paggalang sa mga palakol, na may simula sa CM at sumulong sa CM, mananatili ang parehong form tulad ng para sa paggalaw patungkol sa inertial frame ng sanggunian ( Cm. Inertial frame ng sanggunian). Sa pagtingin sa mga katangiang ito, ang konsepto ng CM ay may mahalagang papel sa dynamics ng isang system at isang matibay na katawan.

S. M. Targ.

Mahusay na Soviet Encyclopedia. - M.: Soviet encyclopedia. 1969-1978 .

Tingnan kung ano ang "Center of Mass" sa iba pang mga dictionary:

- (gitna ng pagkawalang-kilos) ng isang katawan (system ng mga materyal na puntos), isang punto, ang posisyon na nagpapakilala sa pamamahagi ng mga masa sa isang katawan o mekanikal na sistema. Kapag ang isang katawan ay gumagalaw, ang gitna ng masa ay gumagalaw tulad ng isang materyal na punto na may isang masa na katumbas ng masa ng buong katawan, sa ... ... encyclopedic Diksiyonaryo

- (gitna ng pagkawalang-galaw) ng isang katawan (system ng mga materyal na puntos) isang punto na nagpapakilala sa pamamahagi ng masa sa isang katawan o mekanikal na sistema. Kapag ang isang katawan ay gumagalaw, ang gitna ng masa ay gumagalaw tulad ng isang materyal na punto na may isang masa na katumbas ng masa ng buong katawan, kung saan ... ... Malaking Diksyonaryo ng Encyclopedic

sentro ng misa- mekanikal na sistema; gitna ng misa; sangay sentro ng pagkawalang-kilos Geometric point kung saan ang kabuuan ng mga produkto ng masa ng lahat ng mga materyal na puntos na bumubuo ng isang mekanikal na sistema ng kanilang mga radius vector na iginuhit mula sa puntong ito ay katumbas ng zero ... Polytechnic Terminological Explanatory Dictionary

Kapareho ng gitna ng pagkawalang-galaw. Physical encyclopedic na diksyunaryo. M.: Soviet encyclopedia. Punong editor A.M Prokhorov. 1983. CENTER OF THE MASS ... Physical encyclopedia

Ang term na ito ay may iba pang mga kahulugan, tingnan ang Center of gravity (disambiguation). Center ng masa, sentro ng pagkawalang-galaw, barycenter (mula sa ibang Greek na mabigat + κέντρον center) (sa mekanika) isang geometriko na punto na nagpapakilala sa paggalaw ng isang katawan o isang sistema ng mga particle bilang ... ... Wikipedia

sentro ng misa- 3.1 gitna ng masa: Ang isang punto na nauugnay sa isang pisikal na katawan at pagkakaroon ng tulad ng isang pag-aari na ang isang haka-haka point object na may isang masa na katumbas ng masa ng pisikal na katawang ito, na inilagay sa puntong ito, ay magkakaroon ng parehong sandali ng pagkawalang-kilos medyo arbitrary ... ... Aklat na sanggunian sa diksyonaryo ng mga tuntunin ng normative at teknikal na dokumentasyon

Sentro ng pagkawalang-galaw at, point C, na nagpapakilala sa pamamahagi ng masa sa mekanikal. sistema Ang radius ay ang vector ng CM ng isang system na binubuo ng mga materyal na puntos, kung saan ang mi at ri ay ang masa at radius ng vector ng ith point, at ang M ay ang masa ng buong system. Kapag gumagalaw ang system, lilipat ang Ts. M. ... Malaking Encyclopedic Polytechnic Dictionary

- (gitna ng pagkawalang-galaw) ng katawan (system ng mga materyal na puntos), punto, posisyon sa kulub na katangian ng pamamahagi ng mga masa sa katawan o mekanikal. sistema Kapag ang kanyang katawan ay gumagalaw, ang kanyang Cm ay gumagalaw tulad ng isang materyal na punto na may isang masa na katumbas ng masa ng buong katawan, sa isang pangkat ... ... Likas na agham. encyclopedic Diksiyonaryo

Sentro ng misa- (gitna ng pagkawalang-galaw) geometriko point, ang posisyon kung saan nailalarawan ang pamamahagi ng masa sa isang katawan o mekanikal na sistema ... Pisikal na Antropolohiya. Inilarawan ang paliwanag na diksyunaryo.

Isang punto na kumakatawan sa pamamahagi ng masa sa isang katawan o mekanikal na sistema. Kapag ang isang katawan (system) ay gumagalaw, ang CM nito ay gumagalaw tulad ng isang materyal na punto na may isang masa na katumbas ng masa ng buong katawan, kung saan ang lahat ng mga puwersa na kumikilos sa katawang ito ay inilalapat ... Diksyong Astronomiko

Mga libro

• , Weber Alfred. Si Alfred Weber ay isang German sociologist, culturologist, historian, masidhing alam ang kalikasan at direksyon ng kasaysayan ng lipunan at mga uso sa politika. Isang nabigla na saksi sa dalawang sakuna ng Europa ...
• Mga paborito Ang krisis ng kultura ng Europa, Weber A. Alfred Weber (1868-1958) - German sociologist, culturologist, historian, masidhing alam ang kalikasan at direksyon ng kasaysayan ng lipunan at mga uso sa politika. Gulat na saksi sa dalawang sakuna ...

Sa seksyong ito, isasaalang-alang namin nang detalyado ang isang partikular na kaso ng isang sistema ng wastong parallel na pwersa. Namely, anumang materyal na katawan o system ng mga materyal na puntos (discrete particle) na matatagpuan sa Earth ay napapailalim sa pagkilos ng gravity. Samakatuwid, ang lakas ng gravity ay kumikilos sa bawat maliit na butil ng naturang mga mekanikal na sistema. Mahigpit na pagsasalita, ang lahat ng mga puwersang ito ay nakadirekta sa isang punto patungo sa gitna ng Earth. Ngunit dahil ang mga sukat ng mga pang-terrestrial na katawan ay napakaliit sa paghahambing sa radius ng Earth (ipinapalagay namin na ang mga volume na kung saan ang mga discrete particle ay nakapaloob ay maliit din), kung gayon na may isang mataas na antas ng kawastuhan ang mga puwersang ito ay maaaring isaalang-alang na parallel. Ang talata ay nakatuon sa pagbawas ng sistemang ito ng mga puwersa.

Tiyak na grabidad

Piliin natin sa katawan ang isang maliit na butil ng elementarya na may dami na napakaliit na ang posisyon nito ay maaaring matukoy ng isang radius vector Hayaan ang bigat ng maliit na butil na ito ay

ay tinatawag na tiyak na grabidad, at ang dami

Densidad ng katawan.

Sa sistemang SI ng mga yunit, ang tukoy na grabidad ay may sukat

at ang kapal

Sa pangkalahatang kaso, ang tiyak na gravity at density ay mga pagpapaandar ng mga coordinate ng mga punto ng katawan. Kung ang mga ito ay pareho para sa lahat ng mga puntos, pagkatapos ang katawan ay tinatawag na homogenous.

Ang resulta ng lahat ng mga puwersa sa elementarya na gravity ay katumbas ng kanilang kabuuan at kumakatawan sa bigat ng katawan. Ang gitna ng mga kahilera na ito ay tinatawag na sentro ng gravity ng katawan.

Malinaw na, ang posisyon ng gitna ng grabidad sa katawan ay hindi nakasalalay sa oryentasyon ng katawan sa kalawakan. Ang pahayag na ito ay sumusunod mula sa naunang pangungusap na ang gitna ng mga parallel na pwersa ay hindi binabago ang posisyon nito kapag ang lahat ng mga puwersa ay pinaikot ng parehong anggulo sa paligid ng kanilang mga punto ng aplikasyon.

Mga Pormula na Tinutukoy ang Mga Sentro ng Gravity ng isang Katawan at Mga Sistema ng Discrete Particle

Upang matukoy ang gitna ng grabidad ng katawan, hahatiin namin ito sa sapat na maliliit na mga particle na may dami. Sa bawat isa sa kanila inilalapat namin ang puwersa ng gravity na katumbas ng

Ang resulta ng mga kahilera na ito ay katumbas ng bigat ng katawan, na ipinapahiwatig namin sa pamamagitan ng

Ang radius vector ng sentro ng gravity ng katawan, na ipinapahiwatig namin sa pamamagitan ng, ay natutukoy ng mga formula ng nakaraang seksyon bilang sentro ng mga parallel na pwersa. Sa gayon, magkakaroon tayo

Kung ang sentro ng gravity ng isang sistema ng mga discrete particle ay natutukoy, pagkatapos ay magkakaroon ng tiyak na gravity ng maliit na butil, V, - ang dami nito - ang radius vector na tumutukoy sa posisyon ng maliit na butil. Tinutukoy ng huling pormula sa kasong ito ang sentro ng masa ng system ng mga discrete na partikulo.

Kung ang isang mekanikal na sistema ay isang katawan na nabuo ng isang tuluy-tuloy na hanay ng mga particle, pagkatapos sa limitasyon ang mga kabuuan ng huling mga formula ay magiging integral at ang radius vector ng sentro ng gravity ng katawan ay maaaring kalkulahin ng pormula:

kung saan ang mga integral ay ipinamamahagi sa buong dami ng katawan.

Kung ang katawan ay magkakauri, kung gayon ang huling pormula ay:

kung saan ang V ay ang dami ng buong katawan.

Kaya, kapag ang katawan ay homogenous, ang pagpapasiya ng gitna ng grabidad ay nabawasan sa isang purong geometriko na problema. Sa kasong ito, nagsasalita ang isa sa gitna ng gravity ng lakas ng tunog.

Body mass center

Ang ipinakilala na konsepto ng sentro ng grabidad ay makatuwiran lamang para sa mga katawan (maliit kung ihahambing sa mga sukat ng Earth) na matatagpuan malapit sa ibabaw ng Earth. Sa parehong oras, ang paraan ng pagkalkula ng mga coordinate ng gitna ng gravity ay nagbibigay-daan sa iyo upang ilapat ito upang makalkula ang mga coordinate ng isang punto na nagpapakilala sa pamamahagi ng bagay sa katawan. Para sa mga ito, hindi ang bigat ng mga maliit na butil ang dapat isaalang-alang, ngunit ang kanilang masa. Ang bawat maliit na butil ng isang katawan ay may dami ng

at pinapalitan ang dating nakuha na pormula na nakarating kami sa pagkakapantay-pantay:

na tumutukoy sa isang punto na tinatawag na gitna ng masa o gitna ng masa ng katawan.

Kung ang sistema ay binubuo ng mga materyal na puntos, kung saan ang masa, kung gayon ang gitna ng masa ng system ay matatagpuan ng pormula:

nasaan ang masa ng buong sistema. Ang radius vector ng gitna ng masa ng katawan ay nakasalalay sa pagpili ng pinagmulan ng mga coordinate O. Kung ang sentro ng pagkawalang-kilos mismo ay napili bilang pinagmulan ng mga coordinate, pagkatapos ay magiging katumbas ng zero:

Ang konsepto ng gitna ng masa ay maaaring ipakilala nang nakapag-iisa sa konsepto ng sentro ng grabidad. Dahil dito, nabibilang ito sa anumang mekanikal na sistema.

Static sandali

Ang mga expression ay tinatawag, ayon sa pagkakabanggit, ang mga static na sandali ng timbang, dami at masa ng katawan na may kaugnayan sa point O. Kung ang gitna ng masa ng katawan ay napili bilang punto (pinagmulan ng mga coordinate), kung gayon ang mga static na sandali ng katawan na may kaugnayan sa ang gitna ng masa ay magiging katumbas ng zero, na gagamitin ng paulit-ulit sa hinaharap.

Sentro ng Mga Paraan ng Pagkalkula ng Mass

Sa kaso ng isang kumplikadong hugis ng katawan, ang pagpapasiya ng mga coordinate ng gitna ng masa ayon sa naibigay na pangkalahatang mga formula ay karaniwang nauugnay sa mga masusing pagsasaayos. Sa ilang mga kaso, maaari silang mapadali sa pamamagitan ng paggamit ng mga sumusunod na pamamaraan.

1) Paraan ng mahusay na proporsyon. Hayaan ang katawan na magkaroon ng isang sentro ng materyal na mahusay na proporsyon. Nangangahulugan ito na ang bawat maliit na butil na may isang mass at radius vector na iginuhit mula sa gitna na ito ay tumutugma sa isang maliit na butil na may parehong masa at radius vector. Sa kasong ito, ang static moment ng body mass ay mawawala at

Dahil dito, ang gitna ng masa ay magkakasabay sa kasong ito sa gitna ng materyal na mahusay na proporsyon ng katawan. Para sa mga homogenous na katawan, nangangahulugan ito na ang gitna ng masa ay kasabay ng geometric na sentro ng dami ng katawan. Kung ang katawan ay may isang eroplano ng materyal na mahusay na proporsyon, kung gayon ang sentro ng masa ay nasa eroplanong ito. Kung ang katawan ay simetriko tungkol sa axis, kung gayon ang gitna ng masa ay matatagpuan sa axis na ito.

Ang gitna ng masa ay isang punto ng geometriko na matatagpuan sa loob ng isang katawan, na tumutukoy sa pamamahagi ng masa ng katawang ito. Ang anumang katawan ay maaaring kinatawan bilang kabuuan ng isang tiyak na bilang ng mga materyal na puntos. Sa kasong ito, tinutukoy ng posisyon ng gitna ng masa ang radius vector.

Formula 1 - Radius ng gitna ng mass vector.

Ang mi ay ang masa ng kabuuang punto.

ri - radius vector ng pangwakas na punto.

Kung susumahin natin ang masa ng lahat ng mga materyal na puntos, nakukuha natin ang masa ng buong katawan. Ang posisyon ng gitna ng masa ay naiimpluwensyahan ng pagkakapareho ng pamamahagi ng masa sa dami ng katawan. Ang gitna ng masa ay matatagpuan sa loob ng katawan at sa likod ng mga pasilyo nito. Sabihin nating sa singsing, ang gitna ng masa ay nasa gitna ng bilog. Kung saan walang sangkap. Sa pangkalahatan, para sa mga symmetric na katawan na may isang pare-parehong pamamahagi ng masa, ang gitna ng masa ay laging matatagpuan sa gitna ng mahusay na proporsyon o sa axis nito.

Larawan 1 - Mga sentro ng masa ng mga simetriko na katawan.

Kung maglalapat ka ng ilang puwersa sa katawan, magsisimula itong gumalaw. Mag-isip ng isang singsing na nakahiga sa ibabaw ng isang mesa. Kung naglalapat ka ng puwersa dito, ngunit simpleng simulang itulak, pagkatapos ay madulas ito sa ibabaw ng mesa. Ngunit ang direksyon ng paggalaw ay nakasalalay sa lugar kung saan inilalapat ang puwersa.

Kung ang puwersa ay nakadirekta mula sa panlabas na gilid hanggang sa gitna, kasama ang patayo sa panlabas na ibabaw, kung gayon ang singsing ay magsisimulang ilipat nang maayos sa kahabaan ng ibabaw ng mesa sa direksyon ng application ng puwersa. Kung ang isang puwersa ay inilapat nang tangensial sa panlabas na radius ng singsing, pagkatapos ay magsisimulang paikutin ang tungkol sa gitna ng masa. Sa gayon, maaari nating tapusin na ang paggalaw ng katawan ay binubuo ng kabuuan ng galaw ng pagsasalin at ang paggalaw ng paikot na may kaugnayan sa gitna ng masa. Iyon ay, ang paggalaw ng anumang katawan ay maaaring mailarawan sa pamamagitan ng paggalaw ng isang materyal na punto na matatagpuan sa gitna ng masa at pagkakaroon ng masa ng buong katawan.

Larawan 2 - Ang paggalaw ng translational at paikot ng singsing.

Mayroon ding konsepto ng sentro ng grabidad. Sa pangkalahatan, hindi ito pareho sa gitna ng masa. Ang gitna ng grabidad ay ang punto na may kaugnayan sa kung saan ang kabuuang sandali ng grabidad ay zero. Kung naiisip natin ang isang pamalo na may haba na, sabihin nating, 1 metro, isang diameter na 1 cm, at homogenous sa cross section nito. Sa mga dulo ng tungkod, ang mga bola ng metal ng parehong masa ay naayos. Pagkatapos ang gitna ng masa ng pamalo na ito ay nasa gitna. Kung ang tungkod na ito ay inilalagay sa isang hindi nakakapagod na larangan ng gravitational, kung gayon ang sentro ng grabidad ay ililipat patungo sa isang mas mataas na lakas sa bukid.

Larawan 3 - Isang katawan sa isang hindi nakagagalang at magkakatulad na gravitational field.

Sa ibabaw ng mundo, kung saan pare-pareho ang puwersa ng grabidad, ang sentro ng masa ay praktikal na tumutugma sa gitna ng grabidad. Para sa anumang pare-pareho na patlang na gravitational, ang sentro ng grabidad ay palaging magkakasabay sa gitna ng masa.

Ang terminong "sentro ng masa" ay ginagamit hindi lamang sa mekanika at sa mga kalkulasyon ng paggalaw, kundi pati na rin sa pang-araw-araw na buhay. Ito ay lamang na ang mga tao ay hindi palaging nag-iisip tungkol sa kung anong mga batas ng kalikasan ang ipinakita sa isang naibigay na sitwasyon. Halimbawa, ang mga skater ng figure sa pares skating ay aktibong ginagamit ang gitna ng masa ng system kapag pinapagpahinga ang magkahawak na kamay.

Ang konsepto ng gitna ng masa ay ginagamit din sa disenyo ng barko. Kinakailangan na isaalang-alang hindi lamang ang dalawang katawan, ngunit ang isang malaking bilang ng mga ito at dalhin ang lahat sa isang karaniwang denominator. Ang mga pagkakamali sa mga kalkulasyon ay nangangahulugang kakulangan ng katatagan ng barko: sa isang kaso, ito ay labis na malulubog sa tubig, nanganganib na pumunta sa ilalim ng pinakamaliit na alon; at sa kabilang dako, ito ay masyadong nakataas sa taas ng dagat, na lumilikha ng panganib na mabaligtad sa tagiliran nito. Sa pamamagitan ng paraan, iyon ang dahilan kung bakit ang bawat bagay sa board ay dapat na nasa lugar nito, na ibinigay para sa mga kalkulasyon: ang pinaka-napakalaking mga ay nasa pinakailalim.

Ang sentro ng masa ay ginagamit hindi lamang kaugnay sa mga celestial na katawan at ang disenyo ng mga mekanismo, kundi pati na rin sa pag-aaral ng "pag-uugali" ng mga maliit na butil ng microworld. Halimbawa, marami sa kanila ay ipinanganak na pares (electron-positron). Nagtataglay ng paunang pag-ikot at pagsunod sa mga batas ng akit / pagtataboy, maaari silang maituring bilang isang sistema na may isang karaniwang sentro ng masa.