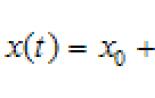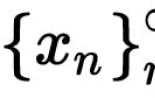Pagkakapantay-pantay ng pagtukoy ng limitasyon sa mga tuntunin ng Hein at Cauchy. Limitasyon ng pagpapaandar. b. Batas sa pag-andar ng base

Limitasyon ng pagpapaandar- numero a ang magiging hangganan ng ilang variable na halaga kung, sa proseso ng pagbabago nito, ang variable na halagang ito ay walang hanggan na lalapit a.

O sa madaling salita, ang bilang A ay ang limitasyon ng pagpapaandar y = f (x) sa puntong ito x 0 kung para sa anumang pagkakasunud-sunod ng mga puntos mula sa domain ng pagpapaandar na hindi katumbas ng x 0, at kung saan nagko-convert sa punto x 0 (lim x n = x0), ang pagkakasunud-sunod ng mga kaukulang halaga ng pag-andar na nagko-convert sa numero A.

Ang graph ng isang pagpapaandar na ang limitasyon para sa isang argument na may kaugaliang sa kawalang-hanggan ay L:

Ibig sabihin PERO ay isang limitasyon (nililimitahan ang halaga) ng pagpapaandar f (x) sa puntong ito x 0 kung para sa anumang pagkakasunud-sunod ng mga puntos na nagko-convert sa x 0 ngunit alin ang hindi naglalaman x 0 bilang isa sa mga elemento nito (ibig sabihin, sa isang nabutas na kapitbahayan x 0), ang pagkakasunud-sunod ng mga halaga ng pagpapaandar nagtatagpo sa A.

Ang limitasyon ng Cauchy ng pagpapaandar.

Ibig sabihin A magiging limitasyon sa pag-andar f (x) sa puntong ito x 0 kung para sa anumang pasulong na kinuha na hindi negatibong numero ε ang katumbas na hindi negatibong numero ay matatagpuan δ = δ(ε) tulad na para sa bawat pagtatalo x nagbibigay-kasiyahan sa kundisyon 0 < | x - x0 | < δ , ang hindi pagkakapantay-pantay | f (x) A |< ε .

Napakadali kung naiintindihan mo ang kakanyahan ng limitasyon at ang mga pangunahing alituntunin para sa paghahanap nito. Ano ang limitasyon ng isang pagpapaandar f (x) sa x inaasam a ay katumbas ng A, ay nakasulat sa ganitong paraan:

Bukod dito, ang halaga na kinabibilangan ng variable x, maaaring hindi lamang isang numero, ngunit pati na rin kawalang-hanggan (∞), minsan + ∞ o -∞, o maaaring walang hangganan sa lahat.

Upang maunawaan kung paano hanapin ang mga limitasyon ng isang pagpapaandar, pinakamahusay na makita ang mga halimbawa ng solusyon.

Kinakailangan upang mahanap ang mga limitasyon ng pagpapaandar f (x) = 1 /x sa:

x→ 2, x→ 0, x→ ∞.

Maghanap tayo ng isang solusyon sa unang limitasyon. Upang magawa ito, maaari mo lamang palitan x ang bilang na kinabibilangan nito, ibig sabihin 2, nakukuha namin:

Hanapin ang pangalawang limitasyon ng pagpapaandar... Dito, palitan ang 0 sa dalisay nitong anyo sa halip x imposible, kasi hindi mo maaaring hatiin sa 0. Ngunit maaari naming kunin ang mga halagang malapit sa zero, halimbawa, 0.01; 0.001; 0,0001; 0.00001 at iba pa, at ang halaga ng pagpapaandar f (x) tataas: 100; 1000; 10000; 100,000 at iba pa. Sa gayon, mauunawaan na para sa x→ 0 ang halaga ng pagpapaandar na nasa ilalim ng limitasyon ng pag-sign ay tataas nang walang katiyakan, ibig sabihin magsumikap para sa kawalang-hanggan. Ibig sabihin nito:

Na patungkol sa pangatlong limitasyon. Ang parehong sitwasyon tulad ng sa nakaraang kaso, imposibleng kapalit ∞ sa dalisay na anyo nito. Kailangan nating isaalang-alang ang kaso ng walang limitasyong pagtaas x... Pinapalitan namin isa-isa ang 1000; 10000; 100000 at iba pa, mayroon kaming halaga ng pagpapaandar f (x) = 1 /x ay babawasan: 0.001; 0,0001; 0.00001; at iba pa, nagkahilig sa zero. Samakatuwid:

Kinakailangan upang makalkula ang limitasyon ng pagpapaandar

Simula upang malutas ang pangalawang halimbawa, nakikita namin ang kawalan ng katiyakan. Mula dito makikita natin ang pinakamataas na antas ng numerator at denominator - ito ay x 3, inilabas namin ito mula sa panaklong sa numerator at denominator at pagkatapos ay binawasan ito ng:

Sagot

Ang unang hakbang sa paghahanap ng hangganan na ito, palitan ang halagang 1 sa halip x, bilang isang resulta kung saan wala kaming katiyakan. Upang malutas ito, isinasaalang-alang namin ang numerator sa mga kadahilanan, gagawin namin ito sa pamamagitan ng pamamaraan ng paghahanap ng mga ugat ng quadratic equation x 2 + 2x - 3:

D = 2 2 - 4 * 1 * (- 3) = 4 +12 = 16→ √ D =√16 = 4

x 1,2 = (-2± 4) / 2→ x 1 = -3;x 2= 1.

Kaya ang bilang ay magiging:

Sagot

Ito ang kahulugan ng tiyak na halaga nito o isang tiyak na lugar, kung saan bumagsak ang pagpapaandar, na kung saan ay limitado ng limitasyon.

Upang malutas ang mga limitasyon, sundin ang mga patakaran:

Ang pagkakaroon ng naunawaan ang kakanyahan at pangunahing mga panuntunan para sa paglutas ng limitasyon, makakakuha ka ng isang pangunahing pag-unawa sa kung paano malutas ang mga ito.

Magsimula tayo sa mga pangkalahatang bagay na napaka-mahalaga, ngunit iilang tao ang nagbibigay pansin sa kanila.

Limitasyon ng pagpapaandar - pangunahing mga konsepto.

Walang hangganang paninindigan simbolo. Sa katunayan, ang infinity ay alinman sa isang walang katapusang malaking positibong numero, o isang walang katapusang malaking negatibong numero.

Ano ang ibig sabihin nito: kapag nakita mo, walang pagkakaiba kung ito ay o. Ngunit mas mahusay na huwag palitan ng, tulad ng mas mahusay na huwag palitan.

Isulat ang limitasyon sa pag-andar f (x) kinuha sa form, ang argumento x ay ipinahiwatig sa ibaba at sa pamamagitan ng arrow sa kung anong halaga ang gusto nito.

Kung ito ay isang tukoy na tunay na numero, pinag-uusapan nila limitasyon ng pagpapaandar sa punto.

Kung o. tapos pinag uusapan nila limitasyon ng pagpapaandar sa kawalang-hanggan.

Ang limitasyon mismo ay maaaring katumbas ng isang tukoy na totoong numero, kung saan sinabi na ang hangganan ay may hangganan.

Kung o tapos sinabi nila yun ang hangganan ay walang hanggan.

Sinasabi din nila yun walang hangganan kung imposibleng matukoy ang tiyak na halaga ng limitasyon o ang walang katapusang halaga nito (, o). Halimbawa, walang limitasyon mula sa sine at infinity.

Limitasyon ng pagpapaandar - pangunahing mga kahulugan.

Oras na para maging busy paghahanap ng mga halaga ng mga limitasyon ng pag-andar sa infinity at sa isang punto. Maraming mga kahulugan ang makakatulong sa amin dito. Ang mga kahulugan na ito ay batay sa mga pagkakasunud-sunod ng bilang at ang kanilang tagpo o pagkakaiba-iba.

Kahulugan(paghahanap ng hangganan ng isang pagpapaandar sa infinity).

Ang bilang A ay tinatawag na limitasyon ng pagpapaandar f (x) sa, kung para sa anumang walang katapusang malaking pagkakasunud-sunod ng mga argumento ng pag-andar (walang katapusang malaking positibo o negatibo), ang pagkakasunud-sunod ng mga halaga ng pagpapaandar na ito ay nagko-convert sa A. Ito ay ipinahiwatig.

Magkomento.

Ang hangganan ng pagpapaandar f (x) sa ay walang hanggan, kung para sa anumang walang katapusang malalaking pagkakasunud-sunod ng mga argumento ng pag-andar (walang katapusang malaking positibo o negatibo), ang pagkakasunud-sunod ng mga halaga ng pagpapaandar na ito ay walang katapusang malaking positibo o walang katapusan na malaking negatibo. Ito ay ipinahiwatig.

Halimbawa.

Gamit ang kahulugan ng limitasyon sa, patunayan ang pagkakapantay-pantay.

Solusyon

Sumulat tayo ng isang pagkakasunud-sunod ng mga halaga ng pag-andar para sa isang walang katapusang malaking positibong pagkakasunud-sunod ng mga halaga ng argument.

Malinaw na, ang mga tuntunin ng pagkakasunud-sunod na ito ay bumababa nang walang pagbabago sa zero.

Ilustrasyong grapiko.

Ngayon ay isulat natin ang pagkakasunud-sunod ng mga halaga ng pag-andar para sa isang walang katapusang malaking negatibong pagkakasunud-sunod ng mga halagang argumento.

Ang mga tuntunin ng pagkakasunud-sunod na ito ay bumababa din nang walang pagbabago sa zero, na nagpapatunay ng orihinal na pagkakapantay-pantay.

Ilustrasyong grapiko.

Halimbawa.

Hanapin ang hangganan

Solusyon

Sumulat tayo ng isang pagkakasunud-sunod ng mga halaga ng pag-andar para sa isang walang katapusang malaking positibong pagkakasunud-sunod ng mga halaga ng argument. Kunin natin, halimbawa.

Ang pagkakasunud-sunod ng mga halaga ng pag-andar ay magiging (mga asul na puntos sa grap)

Malinaw na, ang pagkakasunud-sunod na ito ay walang hanggan malaking positibo, samakatuwid,

Sumulat tayo ngayon ng isang pagkakasunud-sunod ng mga halaga ng pag-andar para sa isang walang katapusang malaking negatibong pagkakasunud-sunod ng mga halaga ng argument. Kunin natin, halimbawa.

Ang pagkakasunud-sunod ng mga halaga ng pag-andar ay magiging (berdeng mga tuldok sa grap)

Malinaw na, ang pagkakasunud-sunod na ito ay nagko-convert sa zero, samakatuwid,

Ilustrasyong grapiko

Sagot:

Ngayon pag-usapan natin ang tungkol sa pagkakaroon at paghanap ng limitasyon ng isang pagpapaandar sa isang punto. Ang lahat ay batay sa pagpapasiya ng unilateral na mga limitasyon... Ang pagkalkula ng mga limitasyong may panig ay kailangang-kailangan para sa.

Kahulugan(paghahanap ng hangganan ng pagpapaandar sa kaliwa).

Ang bilang В ay tinawag na limitasyon ng pagpapaandar f (x) sa kaliwa sa, kung para sa anumang pagkakasunud-sunod ng mga argumento ng pag-andar na nagko-convert sa a, ang mga halaga na mananatiling mas mababa sa isang (), ang pagkakasunud-sunod ng mga halaga ng ang pagpapaandar na ito ay nagko-convert sa B.

Tinalo .

Kahulugan(paghahanap ng hangganan ng pagpapaandar sa kanan).

Ang bilang В ay tinawag na hangganan ng pagpapaandar f (x) sa kanan kung, kung para sa anumang pagkakasunud-sunod ng mga argumento ng pag-andar na nagko-convert sa a, ang mga halaga na mananatiling mas malaki sa isang (), ang pagkakasunud-sunod ng mga halaga ng ang pagpapaandar na ito ay nagko-convert sa B.

Tinalo .

Kahulugan(pagkakaroon ng limitasyon ng isang pagpapaandar sa isang punto).

Ang hangganan ng pagpapaandar f (x) sa puntong a umiiral kung may mga limitasyon sa kaliwa at kanan a at sila ay pantay sa bawat isa.

Magkomento.

Ang hangganan ng pagpapaandar f (x) sa puntong a ay walang hanggan kung ang mga limitasyon sa kaliwa at kanan a ay walang hanggan.

Ipaliwanag natin ang mga kahulugan na ito sa isang halimbawa.

Halimbawa.

Patunayan ang pagkakaroon ng isang may hangganan na limitasyon ng isang pagpapaandar sa puntong ito Hanapin ang kahulugan nito.

Solusyon

Magsisimula kami mula sa kahulugan ng pagkakaroon ng limitasyon ng isang pagpapaandar sa isang punto.

Una, ipinapakita namin na may hangganan sa kaliwa. Upang magawa ito, kumuha ng isang pagkakasunud-sunod ng mga argumento na nagko-convert sa, at. Ang isang halimbawa ng naturang pagkakasunud-sunod ay

Sa figure, ang mga kaukulang halaga ay ipinapakita na may berdeng mga tuldok.

Madaling makita na ang pagkakasunud-sunod na ito ay nagko-convert sa -2, kaya .

Pangalawa, ipinapakita namin na mayroong isang limitasyon sa kanan. Upang magawa ito, kumuha ng isang pagkakasunud-sunod ng mga argumento na nagko-convert sa, at. Ang isang halimbawa ng naturang pagkakasunud-sunod ay

Ang kaukulang pagkakasunud-sunod ng mga halaga ng pag-andar ay magkakaroon ng form

Sa figure, ang mga kaukulang halaga ay ipinapakita na may mga asul na tuldok.

Madaling makita na ang pagkakasunud-sunod na ito ay nagko-convert din sa -2, kaya .

Sa pamamagitan nito ipinakita namin na ang mga limitasyon sa kaliwa at sa kanan ay pantay, samakatuwid, sa pamamagitan ng kahulugan, mayroong isang limitasyon ng pagpapaandar sa puntong ito, at

Ilustrasyong grapiko.

Inirerekumenda namin na ipagpatuloy ang pag-aaral ng mga pangunahing kahulugan ng teorya ng mga limitasyon sa paksa.

Ang mga kahulugan ng hangganan ng isang pag-andar ayon sa Heine (sa mga tuntunin ng pagkakasunud-sunod) at ayon kay Cauchy (sa mga tuntunin ng kapitbahayan ng epsilon at delta) ay ibinigay. Ang mga kahulugan ay ibinibigay sa isang unibersal na form na naaangkop sa parehong bilateral at unilateral na mga limitasyon sa mga endpoint at sa infinity. Ang kahulugan na tumuturo sa a ay hindi ang limitasyon ng isang pagpapaandar ay isinasaalang-alang. Katibayan ng pagkakapareho ng mga kahulugan ng Heine at Cauchy.

Nilalaman

Tingnan din: Point kapitbahayan
Natutukoy ang Limitasyon ng isang Pag-andar sa isang End Point
Natutukoy ang Limitasyon ng isang Pag-andar sa Infinity

Ang unang kahulugan ng limitasyon ng isang pagpapaandar (ayon kay Heine)

(x) sa puntong x 0 :
,
kung
1) mayroong isang nabutas na kapitbahayan ng puntong x 0
2) para sa anumang pagkakasunud-sunod (x n) nagko-convert sa x 0 :
na ang mga elemento ay kabilang sa kapitbahayan,
kasunod (f (x n)) nagko-convert sa isang:
.

Narito x 0 at ang isang ay maaaring parehong may hangganan na mga numero at puntos sa infinity. Ang kapitbahayan ay maaaring maging parehong panig at isang panig.

.

Pangalawang kahulugan ng limitasyon ng isang pagpapaandar (ni Cauchy)

Ang bilang a ay tinatawag na limitasyon ng pagpapaandar f (x) sa puntong x 0 :
,
kung
1) mayroong isang nabutas na kapitbahayan ng puntong x 0 kung saan tinukoy ang pagpapaandar;
2) para sa anumang positibong numero ε > 0 mayroong isang bilang δ ε > 0 nakasalalay sa ε tulad na para sa lahat ng x kabilang sa nabutas δ ε ay isang kapitbahayan ng puntong x 0 :
,
ang mga halaga ng pagpapaandar f (x) nabibilang sa ε - mga kapitbahayan ng point a:
.

Mga Puntong x 0 at ang isang ay maaaring parehong may hangganan na mga numero at puntos sa infinity. Ang kapitbahayan ay maaari ding pareho ng dalawang panig at isang panig.

Isulat natin ang kahulugan na ito gamit ang mga lohikal na simbolo ng pagkakaroon at pagiging unibersal:
.

Ang kahulugan na ito ay gumagamit ng mga kapitbahayan na may mga equidistant na dulo. Ang isang katumbas na kahulugan ay maaari ding ibigay gamit ang di-makatwirang mga kapitbahayan ng mga puntos.

Kahulugan gamit ang di-makatwirang mga kapitbahayan
Ang bilang a ay tinatawag na limitasyon ng pagpapaandar f (x) sa puntong x 0 :
,
kung
1) mayroong isang nabutas na kapitbahayan ng puntong x 0 kung saan tinukoy ang pagpapaandar;
2) para sa anumang kapitbahayan U (a) point a, mayroong isang nabutas na kapitbahayan ng point x 0 tulad na para sa lahat ng x na kabilang sa nabutas na kapitbahayan ng puntong x 0 :
,
ang mga halaga ng pagpapaandar f (x) kabilang sa kapitbahayan U (a) puntos ng:
.

Gamit ang mga lohikal na simbolo ng pagkakaroon at pagiging unibersal, ang kahulugan na ito ay maaaring nakasulat tulad ng sumusunod:
.

Isang-panig at dalawang-panig na mga limitasyon

Ang mga kahulugan sa itaas ay unibersal sa diwa na maaari silang magamit para sa anumang uri ng kapitbahayan. Kung, habang ginagamit namin ang kaliwang panig na nabutas na kapitbahayan ng endpoint, makukuha namin ang kahulugan ng limitasyong kaliwang panig. Kung gagamitin namin ang kapitbahayan ng isang walang katapusang malayong punto bilang isang kapitbahayan, makuha namin ang kahulugan ng limitasyon sa kawalang-hanggan.

Upang matukoy ang hangganan ng Heine, ito ay umuusbong sa katotohanan na ang isang karagdagang paghihigpit ay ipinataw sa isang di-makatwirang pagkakasunud-sunod na nagko-convert - ang mga elemento nito ay dapat na kabilang sa kaukulang nabutas na kapitbahayan ng punto.

Upang matukoy ang Cauchy limit, kinakailangan sa bawat kaso na ibahin ang mga expression sa mga hindi pagkakapantay-pantay gamit ang kaukulang mga kahulugan ng kapitbahayan ng punto.
Tingnan ang "Point Neighborhood".

Ang pagtukoy sa puntong iyon ng a ay hindi ang limitasyon ng isang pagpapaandar

Kadalasan kinakailangan na gamitin ang kundisyon na ang puntong a ay hindi ang limitasyon ng pagpapaandar sa. Bumuo tayo ng mga negasyon para sa mga kahulugan sa itaas. Sa kanila, ipinapalagay namin na ang pagpapaandar f (x) ay tinukoy sa ilang nabutas na kapitbahayan ng puntong x 0 ... Mga puntos a at x 0 ay maaaring maging parehong may takda na mga numero at walang hanggan remote. Ang lahat ng nakasaad sa ibaba ay nalalapat sa parehong mga dalawang-panig at isang panig na mga limitasyon.

Ayon kay Heine.
Bilang a ay hindi ang hangganan ng pagpapaandar f (x) sa puntong x 0 : ,
kung may ganitong pagkakasunud-sunod (x n) nagko-convert sa x 0 :
,
na ang mga elemento ay kabilang sa kapitbahayan,
anong pagkakasunud-sunod (f (x n)) ay hindi nagtatagpo sa isang:
.
.

Ni Cauchy.
Bilang a ay hindi ang hangganan ng pagpapaandar f (x) sa puntong x 0 :
,
kung may positibong bilang ε > 0 , kaya't para sa anumang positibong numero δ > 0 , mayroong isang x na kabilang sa nabutas δ - kapitbahayan ng puntong x 0 :
,
na ang halaga ng pagpapaandar f (x) ay hindi kabilang sa ε - kapitbahayan ng puntong a:
.
.

Siyempre, kung ang puntong a ay hindi ang limitasyon ng pagpapaandar sa, sa gayon hindi ito nangangahulugan na hindi ito maaaring magkaroon ng isang limitasyon. Maaaring may hangganan, ngunit hindi ito katumbas ng a. Posible rin ang kaso kapag ang pagpapaandar ay tinukoy sa isang nabutas na kapitbahayan ng punto, ngunit walang limitasyon sa.

Pag-andar f (x) = kasalanan (1 / x) walang limitasyon bilang x → 0.

Halimbawa, ang pagpapaandar ay tinukoy sa, ngunit walang limitasyon. Kumuha tayo ng isang pagkakasunud-sunod para sa patunay. Nagko-convert ito sa isang punto 0 :. Simula noon.
Sumunod tayo. Nagko-convert din ito sa isang punto 0 :. Ngunit mula noon.
Pagkatapos ang limitasyon ay hindi maaaring maging katumbas ng anumang numero a. Sa katunayan, para sa, mayroong isang pagkakasunud-sunod kung saan. Samakatuwid, ang anumang hindi bilang na numero ay hindi isang limitasyon. Ngunit hindi rin ito isang hangganan, dahil mayroong isang pagkakasunud-sunod.

Pagkakapantay-pantay ng Heine at Cauchy kahulugan ng limitasyon

Teorama
Ang mga kahulugan ng limitasyon ng isang pagpapaandar ni Heine at ni Cauchy ay katumbas.

Patunay

Sa patunay, ipinapalagay namin na ang pagpapaandar ay tinukoy sa ilang nabutas na kapitbahayan ng puntong (may hangganan o walang hanggan na malayo). Ang point a ay maaari ding endpoint o infinity.

Patunay ni Heine ⇒ Cauchy

Hayaan ang pagpapaandar na may limitasyon a sa punto ayon sa unang kahulugan (ni Heine). Iyon ay, para sa anumang pagkakasunud-sunod na kabilang sa nabutas na kapitbahayan ng punto at pagkakaroon ng limitasyon
(1) ,
ang limitasyon ng pagkakasunud-sunod ay isang:
(2) .

Ipakita natin na ang pagpapaandar ay may isang limitasyon ng Cauchy sa isang punto. Iyon ay, para sa lahat mayroong iyan para sa lahat.

Ipagpalagay ang kabaligtaran. Hayaan ang mga kundisyon (1) at (2) nasiyahan, ngunit ang pagpapaandar ay walang limitasyong Cauchy. Iyon ay, may isang bagay na umiiral para sa lahat, kaya't
.

Dalhin, kung saan ang n ay isang natural na numero. Pagkatapos mayroong umiiral, at
.
Sa gayon, nakabuo kami ng isang pagkakasunud-sunod na nagko-convert, ngunit ang limitasyon ng pagkakasunud-sunod ay hindi katumbas ng a. Sumasalungat ito sa teorya ng teorama.

Ang unang bahagi ay napatunayan.

Patunay ni Cauchy ⇒ Heine

Hayaan ang pagpapaandar na may limitasyon a sa punto ayon sa pangalawang kahulugan (ni Cauchy). Iyon ay, para sa sinumang mayroong iyon
(3) para sa lahat .

Ipakita natin na ang pagpapaandar ay may isang limitasyon sa isang punto ayon kay Heine.
Kumuha tayo ng isang di-makatwirang numero. Ayon sa kahulugan ni Cauchy, mayroong isang numero, kaya (3) humahawak.

Kumuha ng isang di-makatwirang pagkakasunud-sunod na pagmamay-ari ng isang nabutas na kapitbahayan at nagko-convert. Sa pamamagitan ng kahulugan ng isang nagkakasabay na pagkakasunud-sunod, para sa anumang mayroon doon
sa
Pagkatapos ito ay sumusunod mula sa (3) na
sa
Dahil totoo ito para sa sinuman, kung gayon
.

Pinatunayan ang teorya.

Mga Sanggunian:
L. D. Kudryavtsev. Ang kurso ng pagsusuri sa matematika. Volume 1.Moscow, 2003.

Tingnan din:

Kahulugan 1. Hayaan E- isang walang hangganang hanay. Kung ang anumang kapitbahayan ay naglalaman ng mga puntos ng set E maliban sa point pero, kung gayon pero tinawag panghuli puntong itinakda E.

Kahulugan 2. (Heinrich Heine (1821-1881)). Hayaan ang pagpapaandar
tinukoy sa set NS at PERO tinawag hangganan pagpapaandar
sa puntong ito (o sa
kung para sa anumang pagkakasunud-sunod ng mga halaga ng argument
nagko-convert sa , ang kaukulang pagkakasunud-sunod ng mga halaga ng pag-andar na nagko-convert sa numero PERO... Nagsusulat sila:
.

Mga halimbawa ng... 1) Pag-andar
ay may hangganan na katumbas ng kasama si, sa anumang punto sa linya ng numero.

Sa katunayan, para sa anumang punto at anumang pagkakasunud-sunod ng mga halaga ng argument
nagko-convert sa at binubuo ng mga bilang maliban sa , ang kaukulang pagkakasunud-sunod ng mga halaga ng pagpapaandar ay mayroong form
, at alam namin na ang pagkakasunud-sunod na ito ay nagko-convert sa kasama si... samakatuwid
.

2) Para sa pagpapaandar

.

Ito ay halata dahil kung
, kung gayon
.

3) Pag-andar ng Dirichlet
ay walang limitasyon sa anumang punto.

Sa katunayan, hayaan
at
at lahat May katuwiran ba ang mga numero. Tapos
para sa lahat n, ganun
... Kung
at lahat Hindi makatuwiran na mga numero, kung gayon
para sa lahat n, ganun
... Nakita namin na ang mga kundisyon ng Kahulugan 2 ay hindi nasiyahan, samakatuwid
wala.

4)
.

Sa katunayan, kumuha ng isang di-makatwirang pagkakasunud-sunod
nagko-convert sa

bilang 2. Pagkatapos. Q.E.D.

Kahulugan 3. (Cauchy (1789-1857)). Hayaan ang pagpapaandar
tinukoy sa set NS at Ang limit point ba ng hanay na ito. Bilang PERO tinawag hangganan pagpapaandar
sa puntong ito (o sa
kung para sa anumang
magkakaroon
, tulad na para sa lahat ng mga halaga ng argument NS nagbibigay-kasiyahan sa hindi pagkakapantay-pantay

,

ang hindi pagkakapantay-pantay ay totoo

.

Nagsusulat sila:
.

Ang kahulugan ng Cauchy ay maaari ding ibigay sa tulong ng mga kapitbahayan, kung napansin natin iyon, at:

hayaan ang pagpapaandar
tinukoy sa set NS at Ang limit point ba ng hanay na ito. Bilang PERO tinawag na limitasyon pagpapaandar
sa puntong ito kung para sa anumang -ang kapitbahayan ng punto PERO
may butas - point kapitbahayan
ganyan
.

Ito ay kapaki-pakinabang upang ilarawan ang kahulugan na ito sa isang figure.

Halimbawa 5.
.

Sa katunayan, kunin
arbitrarily at hanapin
, tulad na para sa lahat NS nagbibigay-kasiyahan sa hindi pagkakapantay-pantay
ang hindi pagkakapantay-pantay na humahawak
... Ang huling hindi pagkakapantay-pantay ay katumbas ng hindi pagkakapantay-pantay
, kaya nakikita natin na sapat na ito upang kunin
... Napatunayan ang pahayag.

Patas

Teorama 1. Ang mga kahulugan ng limitasyon ng isang pagpapaandar ayon sa Heine at Cauchy ay katumbas.

Patunay... 1) Hayaan
ni Cauchy. Patunayan natin na ang parehong numero ay ang limitasyong Heine din.

Kunin natin
arbitraryo Ayon sa Kahulugan 3, mayroong
, tulad na para sa lahat
ang hindi pagkakapantay-pantay na humahawak
... Hayaan
- isang di-makatwirang pagkakasunud-sunod tulad nito
sa
... Tapos may number N tulad na para sa lahat
ang hindi pagkakapantay-pantay na humahawak
, ganun
para sa lahat
, ibig sabihin

ayon kay Heine.

2) Ngayon hayaan
ayon kay Heine. Patunayan natin yan
at ayon kay Cauchy.

Ipagpalagay na kabaligtaran, ibig sabihin Ano
ni Cauchy. Tapos meron
tulad na para sa anumang
magkakaroon
,
at
... Isaalang-alang ang pagkakasunud-sunod
... Para sa tinukoy
at anumang n mayroon

at
... Ibig sabihin nito ay
, bagaman
, ibig sabihin numero PERO ay hindi ang hangganan
sa puntong ito ayon kay Heine. Nakakuha kami ng isang kontradiksyon, na nagpapatunay ng pahayag. Pinatunayan ang teorya.

Teorama 2 (sa pagiging natatangi ng limitasyon). Kung mayroong isang limitasyon ng pagpapaandar sa punto , tapos siya lang ang mag isa.

Patunay... Kung ang limitasyon ay tinukoy ni Heine, kung gayon ang pagiging natatangi nito ay sumusunod mula sa pagiging natatangi ng limitasyon ng pagkakasunud-sunod. Kung ang limitasyon ay tinukoy ng Cauchy, kung gayon ang pagiging natatangi nito ay sumusunod mula sa pagkakapareho ng mga kahulugan ng hangganan ng Cauchy at ni Heine. Pinatunayan ang teorya.

Katulad din sa pamantayan ng Cauchy para sa mga pagkakasunud-sunod, ang pamantayan ng Cauchy para sa pagkakaroon ng limitasyon ng isang function na humahawak. Bago ito pormula, nagbibigay kami

Kahulugan 4. Sinasabing ang pagpapaandar
nasiyahan ang kundisyon ng Cauchy sa puntong ito kung para sa anumang
mayroon

ganyan
at
, ang hindi pagkakapantay-pantay
.

Teorama 3 (Cauchy criterion para sa pagkakaroon ng isang limitasyon). Upang ang pagpapaandar
nagkaroon sa punto may hangganan na limitasyon, kinakailangan at sapat na sa puntong ito ang function ay nasiyahan ang kondisyon ng Cauchy.

Patunay.Kailangan... Hayaan
... Kinakailangan upang mapatunayan iyon
nasiyahan sa puntong ito ang kondisyon ng Cauchy.

Kunin natin
arbitrarily at ilagay
... Sa pamamagitan ng kahulugan ng limitasyon para sa mayroon
, tulad na para sa anumang mga halaga
nagbibigay-kasiyahan sa mga hindi pagkakapantay-pantay
at
, ang hindi pagkakapantay-pantay na humahawak
at
... Tapos

Napatunayan na ang pangangailangan.

Pagkakasunud-sunod... Hayaan ang pagpapaandar
nasiyahan sa puntong ito ang kondisyon ng Cauchy. Kinakailangan na patunayan na mayroon ito sa puntong ito huling hangganan

Kunin natin
arbitraryo Sa kahulugan 4, mayroong
, tulad ng mga hindi pagkakapantay-pantay
,
sumusunod dito
- ito ay ibinigay.

Ipakita muna natin iyon para sa anumang pagkakasunud-sunod
nagko-convert sa , kasunod
nagtatagpo ang mga halaga ng pagpapaandar. Sa katunayan, kung
, pagkatapos, sa bisa ng kahulugan ng limitasyon ng pagkakasunud-sunod, para sa isang naibigay
may number N tulad na para sa anumang

at
... Dahil ang
sa puntong ito nasiyahan ang kondisyon ng Cauchy, mayroon kami
... Pagkatapos, sa pamamagitan ng pamantayan ng Cauchy para sa mga pagkakasunud-sunod, ang pagkakasunud-sunod
nagtatagpo. Ipakita natin sa lahat ang mga nasabing pagkakasunud-sunod
magtagpo sa parehong limitasyon. Ipagpalagay na kabaligtaran, ibig sabihin ano ang mga pagkakasunud-sunod
at
,
,
, ganyan. Isaalang-alang ang pagkakasunud-sunod. Malinaw na nagko-convert ito sa , samakatuwid, sa pamamagitan ng kung ano ang napatunayan sa itaas, ang pagkakasunud-sunod ay nagtatagpo, na imposible, dahil sa mga sumunod
at
may magkakaibang mga limitasyon at ... Ipinapakita ng nagreresultang kontradiksyon na =... Samakatuwid, sa pamamagitan ng kahulugan ni Heine, ang pagpapaandar ay nasa punto huling hangganan Ang kasapatan, at samakatuwid ang teorama, ay napatunayan.

Hayaan ang pagpapaandar y = ƒ (x) na tinukoy sa ilang kapitbahayan ng puntong x o, maliban, marahil, ang puntong x o mismo.

Bumuo tayo ng dalawa, katumbas ng bawat isa, mga kahulugan ng limitasyon ng isang pagpapaandar sa isang punto.

Kahulugan 1 (sa "wika ng mga pagkakasunud-sunod", o Heine).

Ang bilang A ay tinatawag na limitasyon ng pagpapaandar y = ƒ (x) sa pugon x 0 (o para sa x® x o) kung para sa anumang pagkakasunud-sunod ng mga tinatanggap na halaga ng argumento x n, n є N (x n ¹ x 0), nagko-convert sa x о, ang pagkakasunud-sunod ng mga kaukulang halaga ng pag-andar ƒ (x n), n є N, nagko-convert sa bilang А

Sa kasong ito, sumulat
o ƒ (x) -> A bilang x → x o. Ang kahulugan ng geometriko ng limitasyon ng isang pag-andar: nangangahulugan na para sa lahat ng mga puntos x sapat na malapit sa puntong x o, ang mga kaukulang halaga ng pagpapaandar ay naiiba na nagkakaiba-iba mula sa bilang A.

Kahulugan 2 (sa "wika ε", o ayon kay Cauchy).

Ang isang bilang A ay tinatawag na limitasyon ng isang pagpapaandar sa isang puntong x o (o bilang x → x o) kung para sa anumang positibo ε mayroong positibong numero δ tulad na para sa lahat ng x¹ x o nasiyahan ang hindi pagkakapantay-pantay | x-x o |<δ, выполняется неравенство |ƒ(х)-А|<ε.

Ang kahulugan ng geometriko ng limitasyon ng isang pagpapaandar:

kung para sa anumang neighborhood-kapitbahayan ng puntong A mayroong isang δ-kapitbahayan ng point xo tulad na para sa lahat ng x¹ x0 mula sa δ-kapitbahayan na ito ang kaukulang halaga ng pagpapaandar ƒ (x) nakasalalay sa ε-kapitbahayan ng A. Sa madaling salita, ang mga puntos ng grap ng pagpapaandar y = ƒ (x) ay namamalagi sa loob ng isang strip ng lapad 2ε, na nalilimitahan ng mga tuwid na linya y = A + ε, y = A-ε (tingnan ang Larawan 110) . Malinaw na, ang halaga ng δ ay nakasalalay sa pagpili ng ε, kaya't nagsusulat sila ng δ = δ (ε).

<< Пример 16.1

Patunayan mo yan

Solusyon: Kumuha ng di-makatwirang ε> 0, hanapin ang δ = δ (ε)> 0 na para sa lahat ng nagbibigay-kasiyahan sa hindi pagkakapantay-pantay | х-3 |< δ, выполняется неравенство |(2х-1)-5|<ε, т. е. |х-3|<ε.

Pagkuha ng δ = ε / 2, nakikita natin iyon para sa lahat na nagbibigay-kasiyahan sa hindi pagkakapantay-pantay | х-3 |< δ, выполняется неравенство |(2х-1)-5|<ε. Следовательно, lim(2x-1)=5 при х –>3.

<< Пример 16.2

16.2. Isang-panig na mga limitasyon

Sa kahulugan ng limitasyon ng pagpapaandar, isinasaalang-alang na ang x ay may gawi sa x 0 sa anumang paraan: natitirang mas mababa sa x 0 (sa kaliwa ng x 0), mas malaki kaysa sa xo (sa kanan ng xo), o oscillating sa paligid ng puntong x 0.

May mga kaso kung kailan ang paraan ng pagtatantya ng argumento x hanggang x o ay makabuluhang nakakaapekto sa halaga ng side-limit ng pagpapaandar. Samakatuwid, ang konsepto ng isang panig na mga limitasyon ay ipinakilala.

Ang bilang A 1 ay tinawag na limitasyon ng pagpapaandar y = ƒ (x) sa kaliwa sa puntong xo kung para sa anumang numero ε> 0 mayroong umiiral na isang numero δ = δ (ε)> 0 na para sa x є (x 0 -δ; xo), ang hindi pagkakapantay-pantay | ƒ (x) -A |<ε. Предел слева записывают так: limƒ(х)=А при х–>x 0 -0 o ilang sandali: ƒ (x o-0) = A 1 (Dirichlet designation) (tingnan ang Larawan 111).

Ang limitasyon ng pagpapaandar sa kanan ay natutukoy sa isang katulad na paraan, isinusulat namin ito gamit ang mga simbolo:

Sa madaling sabi ang limit sa kanan ay tinukoy ng ƒ (x o +0) = A.

Ang mga limitasyon ng isang pagpapaandar sa kaliwa at sa kanan ay tinatawag na isang-panig na mga limitasyon. Malinaw na, kung mayroon, kung gayon ang parehong mga limitasyong may panig ay mayroon, at A = A 1 = A 2.

Ang pag-uusap ay totoo din: kung ang parehong mga limitasyon ƒ (x 0 -0) at ƒ (x 0 +0) ay mayroon at pantay ang mga ito, pagkatapos ay mayroong isang limitasyon at A = ƒ (x 0 -0).

Kung А 1 ¹ А 2, kung gayon ang kapilya na ito ay wala.

16.3. Ang limitasyon ng isang pagpapaandar bilang x ® ∞

Hayaan ang pagpapaandar y = ƒ (x) na tinukoy sa agwat (-∞; ∞). Ang numerong A ay tinawag limitasyon sa pag-andarƒ (x) sa x → ∞ kung para sa anumang positibong numero ε mayroong umiiral na numero<ε. Коротко это определение можно записать так:

Ang kahulugan ng geometriko ng kahulugan na ito ay ang mga sumusunod: para sa "ε> 0 $ M> 0 na para sa x є (-∞; -M) o x є (M; + ∞) ang mga katumbas na halaga ng pagpapaandar ƒ ( x) mahulog sa neighborhood-kapitbahayan ng puntong A, iyon ay, ang mga puntos ng grap ay namamalagi sa isang strip ng lapad 2ε, na nalilimitahan ng mga tuwid na linya y = A + ε at y = A-ε (tingnan ang Larawan 112 ).

16.4. Walang katapusang malaking pag-andar (b.b.f.)

Ang pagpapaandar y = ƒ (x) ay tinatawag na walang katapusang malaki bilang x → x 0 kung para sa anumang bilang na M> 0 mayroong isang bilang δ = δ (M)> 0, na para sa lahat x nasiyahan ang hindi pagkakapantay-pantay 0<|х-хо|<δ, выполняется неравенство |ƒ(х)|>M.

Halimbawa, ang pagpapaandar y = 1 / (x-2) ay b.b.f. para sa x -> 2.

Kung ang ƒ (x) ay may gawi sa infinity bilang x → x o at tumatagal lamang ng mga positibong halaga, nagsusulat sila

kung negatibong halaga lang, kung gayon

Ang pagpapaandar y = ƒ (x), na ibinigay sa buong linya ng numero, tinawag walang hanggan malaki bilang x → ∞, kung para sa anumang bilang na M> 0 mayroong isang bilang na N = N (M)> 0 na para sa lahat x nagbibigay-kasiyahan sa hindi pagkakapantay-pantay | x |> N, ang hindi pagkakapantay-pantay | ƒ (x) |> M ay humahawak. Maikli:

Halimbawa, y = 2x ay b.b.f. bilang x → ∞.

Tandaan na kung ang argumento x, na may gawi sa kawalang-hanggan, ay tumatagal lamang ng mga likas na halaga, ibig sabihin, xєN, kung gayon ang kaukulang b.b.f. ay nagiging isang walang hanggan malaking pagkakasunud-sunod. Halimbawa, ang pagkakasunud-sunod v n = n 2 +1, n є N, ay isang walang katapusang malaking pagkakasunud-sunod. Malinaw na, ang anumang b.b.f. sa isang kapitbahayan ng puntong x o ay walang hanggan sa kapitbahayan na ito. Ang pahayag na pinag-uusapan ay hindi totoo: ang isang walang limitasyong pagpapaandar ay maaaring hindi isang b.b.f. (Halimbawa, y = xsinx.)

Gayunpaman, kung ang limƒ (x) = A bilang x → x 0, kung saan ang A ay isang may hangganan na numero, kung gayon ang pagpapaandar ƒ (x) ay nakagapos sa isang kapitbahayan ng puntong x o.

Sa katunayan, sumusunod ito mula sa kahulugan ng limitasyon ng isang pagpapaandar na bilang x → x 0 ang kundisyon | ƒ (x) -A |<ε. Следовательно, А-ε<ƒ(х)<А+ε при х є (х о -ε; х о +ε), а это и означает, что функция ƒ (х) ограничена.