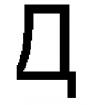Trigonometric series at ang kanilang mga katangian. trigonometriko serye. Fourier serye. Convergence ng Fourier series sa isang punto
Ang kalagayan ni Hölder. Sinasabi namin na ang isang function na $f(x)$ ay nakakatugon sa mga kundisyon ng Hölder sa isang puntong $x_0$ kung mayroong isang panig na may hangganan na mga limitasyon $f(x_0 \pm 0)$ at mga naturang numero $\delta > 0$, $\ alpha \in ( 0,1]$ at $c_0 > 0$ na $|f(x_0+t)-f(x_0+0)|\leq c_0t^( \alpha )$, $|f(x_0-t )-f(x_0-0)|\leq c_0t^(\alpha )$.
Dirichlet formula. Ang binagong formula ng Dirichlet ay tinatawag na pormula ng anyo:
$$S_n(x_0)= \frac(1)(\pi)\int\limits_(0)^(\pi)(f(x_0+t)+f(x_0-t))D_n(t)dt \quad (1),$$ kung saan $D_n(t)=\frac(1)(2)+ \cos t + \ldots+ \cos nt = \frac(\sin(n+\frac(1)(2))t) (2\sin\frac(t)(2)) (2)$ — .
Gamit ang mga formula na $(1)$ at $(2)$, isinusulat namin ang bahagyang kabuuan ng seryeng Fourier sa sumusunod na anyo:
$$S_n(x_0)= \frac(1)(\pi)\int\limits_(0)^(\pi)\frac(f(x_0+t)+f(x_0-t))(2\sin\ frac(t)(2))\sin \kaliwa (n+\frac(1)(2) \kanan) t dt$$
$$\Rightarrow \lim\limits_(n \to \infty )S_n(x_0) — \frac(1)(\pi)\int\limits_(0)^(\pi)\frac(f(x_0+t) +f(x_0-t))(2\sin\frac(t)(2)) \cdot \\ \cdot \sin \left (n+\frac(1)(2) \right)t dt = 0 \quad (3)$$
Para sa $f \equiv \frac(1)(2)$ ang formula na $(3)$ ay nagiging: $$ \lim\limits_(n \to \infty )\frac(1)(\delta)\frac(\ sin (n+\frac(1)(2))t)(2\sin\frac(t)(2))dt=\frac(1)(2), 0
Convergence ng Fourier series sa isang punto
Teorama. Hayaan ang $f(x)$ na maging isang $2\pi$-periodic absolutely integrable function sa $[-\pi,\pi]$ at matugunan ang Hölder condition sa puntong $x_0$. Pagkatapos, ang Fourier series ng function na $f(x)$ sa puntong $x_0$ ay nagtatagpo sa numerong $$\frac(f(x_0+0)+f(x_0-0))(2).$$
Kung sa puntong $x_0$ ang function na $f(x)$ ay tuloy-tuloy, sa puntong ito ang kabuuan ng serye ay katumbas ng $f(x_0)$.
Patunay
Dahil ang function na $f(x)$ ay nakakatugon sa kondisyon ng Hölder sa puntong $x_0$, pagkatapos ay para sa $\alpha > 0$ at $0< t$ $ < \delta$ выполнены неравенства (1), (2).
Para sa isang naibigay na $\delta > 0$, isinusulat namin ang mga pagkakapantay-pantay na $(3)$ at $(4)$. Ang pag-multiply ng $(4)$ sa $f(x_0+0)+f(x_0-0)$ at pagbabawas ng resulta mula sa $(3)$, makakakuha tayo ng $$ \lim\limits_(n \to \infty) (S_n (x_0) - \frac(f(x_0+0)+f(x_0-0))(2) - \\ - \frac(1)(\pi)\int\limits_(0)^(\delta)\ frac(f(x_0+t)+f(x_0-t)-f(x_0+0)-f(x_0-0))(2\sin \frac(t)(2)) \cdot \\ \cdot \ sin \left (n + \frac(1)(2) \right)t \, dt) = 0. \quad (5)$$
Ito ay sumusunod mula sa kondisyon ni Hölder na ang function na $$\Phi(t)= \frac(f(x_0+t)+f(x_0-t)-f(x_0+0)-f(x_0-0))(2\ sin \frac(t)(2)).$$ ay ganap na maisasama sa $$. Sa katunayan, ang paglalapat ng hindi pagkakapantay-pantay ni Hölder, nakuha namin na ang sumusunod na hindi pagkakapantay-pantay ay may hawak para sa function na $\Phi(t)$: $|\Phi(t)| \leq \frac(2c_0t^(\alpha ))(\frac(2)(\pi)t) = \pi c_0t^(\alpha - 1) (6)$, kung saan $\alpha \in (0,1 ]$.
Dahil sa pamantayan ng paghahambing para sa mga hindi wastong integral, ang hindi pagkakapantay-pantay na $(6)$ ay nagpapahiwatig na ang $\Phi(t)$ ay ganap na maisasama sa $.$
Sa pamamagitan ng lemma ni Riemann $$\lim\limits_(n \to \infty)\int\limits_(0)^(\delta)\Phi(t)\sin \left (n + \frac(1)(2) \ right )t\cdot dt = 0 .$$
Mula sa formula na $(5)$ sumusunod na ngayon na $$\lim\limits_(n \to \infty)S_n(x_0) = \frac(f(x_0+0)+f(x_0-0))(2) .$$
[tago]
Bunga 1. Kung ang isang $2\pi$-periodic at ganap na maisasama sa $[-\pi,\pi]$ function na $f(x)$ ay may derivative sa isang puntong $x_0$, kung gayon ang Fourier series nito ay nagtatagpo sa puntong ito sa $f (x_0) $.
Bunga 2. Kung ang isang $2\pi$-periodic at ganap na maisasama sa $[-\pi,\pi]$ function na $f(x)$ ay may parehong one-sided derivatives sa puntong $x_0$, kung gayon ang Fourier series nito ay nagtatagpo sa puntong ito hanggang $\frac (f(x_0+0)+f(x_0-0))(2).$
Bunga 3. Kung ang isang $2\pi$-periodic at ganap na maisasama sa $[-\pi,\pi]$ function na $f(x)$ ay nakakatugon sa kondisyon ng Hölder sa mga puntong $-\pi$ at $\pi$, kung gayon, dapat bayaran sa periodicity, ang kabuuan ng seryeng The Fourier transform sa mga puntong $-\pi$ at $\pi$ ay katumbas ng $$\frac(f(\pi-0)+ f(-\pi+0))( 2).$$
Dini sign
Kahulugan. Hayaan ang $f(x)$ na maging isang $2\pi$-periodic function. Ang puntong $x_0$ ay magiging regular na punto ng function na $f(x)$ kung
- 1) may hangganan ang kaliwa at kanang limitasyon $\lim\limits_(x \to x_0+0 )f(x)= \lim\limits_(x \to x_0-0 )f(x)= f(x_0+0) = f(x_0-0),$
- 2) $f(x_0)=\frac(f(x_0+0)+f(x_0-0))(2).$
Teorama. Hayaang ang $f(x)$ ay isang $2\pi$-periodic absolutely integrable function sa $[-\pi,\pi]$ at ang point na $x_0 \in \mathbb(R)$ ay isang regular na punto ng function na $ f(x)$ . Hayaang matugunan ng function na $f(x)$ ang mga kundisyon ng Dini sa puntong $x_0$: mayroong mga hindi tamang integral $$\int\limits_(0)^(h)\frac(|f(x_0+t)-f( x_0+0) |)(t)dt, \\ \int\limits_(0)^(h)\frac(|f(x_0-t)-f(x_0-0)|)(t)dt,$$
pagkatapos ay ang Fourier series ng function na $f(x)$ sa puntong $x_0$ ay may kabuuan na $f(x_0)$, i.e. $$ \lim\limits_(n \to \infty )S_n(x_0)=f(x_0)=\frac(f(x_0+0)+f(x_0-0))(2).$$
Patunay
Ang bahagyang kabuuan na $S_n(x)$ ng seryeng Fourier ay may mahalagang representasyon na $(1)$. At dahil sa pagkakapantay-pantay na $\frac(2)(\pi )\int\limits_(0)^(\pi )D_n(t) \, dt=1,$
$$ f(x_0)= \frac(1)(\pi )\int\limits_(0)^(\pi )f(x_0+0)+f(x_0-0)D_n(t) \, dt$$
Pagkatapos ay mayroon kaming $$S_n(x_0)-f(x_0) = \frac(1)(\pi)\int\limits_(0)^(\pi)(f(x_0+t)-f(x_0+0) ) D_n(t) \, dt + $$ $$+\frac(1)(\pi)\int\limits_(0)^(\pi)(f(x_0-t)-f(x_0-0)) D_n (t) \, dt. \quad(7)$$
Malinaw, ang theorem ay mapapatunayan kung patunayan natin na ang parehong integral sa formula na $(7)$ ay may mga limitasyon bilang $n \to \infty $ na katumbas ng $0$. Isaalang-alang ang unang integral: $$I_n(x_0)=\int\limits_(0)^(\pi)(f(x_0+t)-f(x_0+0))D_n(t)dt. $$
Ang kondisyon ng Dini ay nasiyahan sa puntong $x_0$: ang hindi wastong integral $$\int\limits_(0)^(h)\frac(|f(x_0+t)-f(x_0+0)|)(t) \, dt .$$
Samakatuwid, para sa anumang $\varepsilon > 0$, mayroong $\delta \in (0, h)$ na $$\int\limits_(0)^(\delta )\frac(\left | f(x_0+ t) -f(x_0+0) \kanan |)(t)dt
Dahil sa napiling $\varepsilon > 0$ at $\delta > 0$, ang integral na $I_n(x_0)$ ay maaaring katawanin bilang $I_n(x_0)=A_n(x_0)+B_n(x_0)$, kung saan
$$A_n(x_0)=\int\limits_(0)^(\delta )(f(x_0+t)-f(x_0+0))D_n(t)dt ,$$ $$B_n(x_0)=\ int\limits_(\delta)^(\pi )(f(x_0+t)-f(x_0+0))D_n(t)dt .$$
Isaalang-alang muna ang $A_n(x_0)$. Gamit ang $\left | D_n(t)\kanan |
para sa lahat ng $t \in (0, \delta)$.
Samakatuwid $$A_n(x_0) \leq \frac(\pi)(2) \int\limits_(0)^(\delta ) \frac(|f(x_0+t)-f(x_0+0)|)( t) dt
Ipasa natin sa pagtantya ang integral na $B_n(x_0)$ bilang $n \to \infty $. Upang gawin ito, ipinakilala namin ang function na $$ \Phi (t)=\left\(\begin(matrix)
\frac(f(x_0+t)-f(x_0+0))(2\sin \frac(t)(2)), 0
$$B_n(x_0)=\int\limits_(-\pi)^(\pi)\Phi (t) \sin \left (n+\frac(1)(2) \right)t\,dt.$$ Nakukuha namin ang $\lim\limits_(n \to \infty )B_n(x_0)=0$, na nangangahulugang para sa isang arbitrary na $\varepsilon > 0$ na pinili nang mas maaga, mayroong $N$ na para sa lahat ng $n> N$ ang hindi pagkakapantay-pantay $|I_n(x_0)|\leq |A_n(x_0)| + |B_n(x_0)|
Ito ay pinatunayan sa eksaktong parehong paraan na ang pangalawang integral ng formula na $(7)$ ay may zero na limitasyon bilang $n \to \infty $.
[tago]
Bunga Kung ang isang $2\pi$ periodic function na $f(x)$ ay piecewise differentiable sa $[-\pi,\pi]$, ang Fourier series nito sa anumang punto ay $x \in [-\pi,\pi]$ ay nagtatagpo sa numerong $$\frac(f(x_0+0)+f(x_0-0))(2).$$
Sa segment na $[-\pi,\pi]$ hanapin ang trigonometric Fourier series ng function na $f(x)=\left\(\begin(matrix)
1, x \in (0,\pi),\\ -1, x \in (-\pi,0),
\\ 0, x=0.
\end(matrix)\right.$
Siyasatin ang convergence ng resultang serye.
Pana-panahong nagpapalawak ng $f(x)$ sa buong totoong axis, nakukuha namin ang function na $\widetilde(f)(x)$, na ang graph ay ipinapakita sa figure.
Dahil kakaiba ang function na $f(x)$, $$a_k=\frac(1)(\pi)\int\limits_(-\pi)^(\pi)f(x)\cos kx dx =0 ; $$
$$b_k=\frac(1)(\pi)\int\limits_(-\pi)^(\pi)f(x)\sin kx \, dx = $$ $$=\frac(2)(\ pi)\int\limits_(0)^(\pi)f(x)\sin kx \, dx =$$ $$=-\frac(2)(\pi k)(1- \cos k\pi) $$
$$b_(2n)=0, b_(2n+1) = \frac(4)(\pi(2n+1)).$$
Samakatuwid, $\tilde(f)(x)\sim \frac(4)(\pi)\sum_(n=0)^(\infty)\frac(\sin(2n+1)x)(2n+1 ).$
Dahil umiiral ang $(f)"(x)$ para sa $x\neq k \pi$, pagkatapos ay $\tilde(f)(x)=\frac(4)(\pi)\sum_(n=0)^ ( \infty)\frac(\sin(2n+1)x)(2n+1)$, $x\neq k \pi$, $k \in \mathbb(Z).$
Sa mga puntong $x=k \pi$, $k \in \mathbb(Z)$, ang function na $\widetilde(f)(x)$ ay hindi tinukoy, at ang kabuuan ng Fourier series ay katumbas ng zero.
Ang pagtatakda ng $x=\frac(\pi)(2)$, makuha namin ang equality $1 — \frac(1)(3) + \frac(1)(5)- \ldots + \frac((-1)^ n) (2n+1)+ \ldots = \frac(\pi)(4)$.
[tago]
Hanapin ang seryeng Fourier ng sumusunod na $2\pi$-periodic at ganap na maisasama sa $[-\pi,\pi]$ function:
$f(x)=-\ln |
\sin \frac(x)(2)|$, $x \neq 2k\pi$, $k \in \mathbb(Z)$, at suriin ang resultang serye para sa convergence.
Dahil ang $(f)"(x)$ ay umiiral para sa $ x \neq 2k \pi$, ang Fourier series ng function na $f(x)$ ay magsasama-sama sa lahat ng punto ng $ x \neq 2k \pi$ sa halaga ng function. Malinaw na ang $f(x)$ ay isang even function at samakatuwid ang Fourier expansion nito ay dapat maglaman ng mga cosine. \sin \frac(x)(2)dx = $$ $$= -2 \int\limits_(0 )^(\frac(\pi)(2))\ln \sin \frac(x)(2) dx \,- \, 2\int\limits_(\frac(\pi)(2))^(\ pi)\ln \sin \frac(x)(2)dx =$$ $$= -2 \int \limits_(0)^(\frac(\pi)(2))\ln \sin \frac(x )(2)dx \, — \, 2\int\limits_(0)^(\frac(\pi )(2))\ln\cos \frac(x)(2)dx=$$ $$= - 2 \int\limits_(0)^(\frac(\pi)(2))\ln (\frac (1)(2)\sin x)dx =$$ $$= \pi \ln 2 \, — \, 2 \int\limits_(0)^(\frac(\pi)(2))\ln \ sin x dx =$$ $$= \pi \ln 2 \, — \, \int\limits_(0 )^(\pi)\ln \sin \frac(t)(2)dt = \pi\ln 2 + \frac(\pi a_0)(2),$$ kung saan ang $a_0= \pi \ln 2$.
Hanapin natin ngayon ang $a_n$ para sa $n \neq 0$. Mayroon kaming $$\pi a_n = -2 \int\limits_(0)^(\pi)\cos nx \ln \sin \frac(x)(2)dx = $$ $$ = \int\limits_(0 ) ^(\pi) \frac(\sin(n+\frac(1)(2))x+\sin (n-\frac(1)(2))x)(2n \sin\frac(x)(2 ) )dx=$$ $$= \frac(1)(2n) \int\limits_(-\pi)^(\pi) \begin(bmatrix)
D_n(x)+D_(n-1)(x)\\ \end(bmatrix)dx.$$
Narito ang $D_n(x)$ ay ang Dirichlet kernel na tinukoy ng formula (2) at nakuha natin na $\pi a_n = \frac(\pi)(n)$ at, dahil dito, $a_n = \frac(1)(n ) $. Kaya $$-\ln |
\sin \frac(x)(2)| = \ln 2 + \sum_(n=1)^(\infty ) \frac(\cos nx)(n), x \neq 2k\pi, k \in \mathbb(Z).$$
[tago]
Panitikan
- Lysenko Z.M., lecture notes sa mathematical analysis, 2015-2016
- Ter-Krikorov A.M. at Shabunin M.I. Kurso ng mathematical analysis, pp. 581-587
- Demidovich B.P., Koleksyon ng mga gawain at pagsasanay sa mathematical analysis, edisyon 13, binago, CheRo Publishing House, 1997, pp. 259-267
Limitasyon sa oras: 0
Navigation (mga numero ng trabaho lamang)
0 sa 5 gawain ang natapos
Impormasyon
Pagsubok sa materyal ng paksang ito:
Nakapag-test ka na dati. Hindi mo na ito maaaring patakbuhin muli.
Naglo-load ang pagsubok...
Dapat kang mag-login o magparehistro upang simulan ang pagsubok.
Dapat mong kumpletuhin ang mga sumusunod na pagsubok upang simulan ang isang ito:
resulta
Mga tamang sagot: 0 sa 5
Oras mo:
Tapos na ang oras
Nakakuha ka ng 0 sa 0 puntos (0 )
Ang iyong marka ay naitala sa leaderboard
- Na may sagot
- Naka-check out
Gawain 1 ng 5
1 .
Bilang ng mga puntos: 1Kung ang isang $2\pi$ -periodic at ganap na maisasama sa $[−\pi,\pi]$ function na $f(x)$ ay may derivative sa puntong $x_0$, kung gayon ano ang pagsasama-sama ng seryeng Fourier nito sa puntong ito ?
Gawain 2 ng 5
2 .
Bilang ng mga puntos: 1Kung ang lahat ng mga kondisyon ng Dini test ay nasiyahan, kung gayon sa anong numero ang Fourier series ng function na $f$ ay nagtatagpo sa puntong $x_0$?
Sa pamamagitan ng mga cosine at sine ng maramihang mga arko, ibig sabihin, isang serye ng anyo
o sa kumplikadong anyo
saan isang k,b k o, ayon sa pagkakabanggit, c k tinawag coefficients ng T. r.
Sa unang pagkakataon T. r. magkita sa L. Euler (L. Euler, 1744). Nakakuha siya ng mga pagpapalawak
Lahat ng R. Ika-18 siglo May kaugnayan sa pag-aaral ng problema ng libreng panginginig ng boses ng isang string, ang tanong ay lumitaw sa posibilidad na kumatawan sa function na nagpapakilala sa paunang posisyon ng string bilang isang kabuuan ng T. r. Ang tanong na ito ay nagdulot ng isang mainit na debate na tumagal ng ilang dekada, ang pinakamahusay na mga analyst ng panahong iyon - D. Bernoulli, J. D "Alembert, J. Lagrange, L. Euler ( L. Euler). Mga pagtatalo na may kaugnayan sa nilalaman ng konsepto ng function. Sa oras na iyon, ang mga function ay karaniwang nauugnay sa kanilang analytics. pagtatalaga, na humantong sa pagsasaalang-alang lamang ng analytic o piecewise analytic function. At dito naging kinakailangan para sa isang function na ang graph ay sapat na arbitrary upang makabuo ng isang T. r. na kumakatawan sa function na ito. Ngunit ang kahalagahan ng mga pagtatalo na ito ay mas malaki. Sa katunayan, tinalakay o bumangon sila kaugnay ng mga tanong na may kaugnayan sa maraming mahahalagang konsepto at ideya ng matematika. pagsusuri sa pangkalahatan - ang representasyon ng mga function ng Taylor series at analytical. pagpapatuloy ng mga pag-andar, paggamit ng magkakaibang serye, mga limitasyon, walang katapusang sistema ng mga equation, mga pag-andar ng polynomial, atbp.
At sa hinaharap, tulad ng sa paunang ito, ang teorya ng T. r. nagsilbing mapagkukunan ng mga bagong ideya sa matematika. Fourier integral, halos pana-panahong mga function, pangkalahatang orthogonal series, abstract . Mga pananaliksik sa T. ilog. nagsilbing panimulang punto para sa paglikha ng set theory. T. r. ay isang makapangyarihang tool para sa pagrepresenta at paggalugad ng mga feature.
Ang tanong na humantong sa kontrobersya sa mga mathematician noong ika-18 siglo ay nalutas noong 1807 ni J. Fourier, na nagpahiwatig ng mga pormula para sa pagkalkula ng mga coefficient ng T. r. (1), na dapat. kumakatawan sa function na f(x):
at inilapat ang mga ito sa paglutas ng mga problema sa pagpapadaloy ng init. Ang mga pormula (2) ay tinatawag na mga pormula ng Fourier, bagama't sila ay nakatagpo ng mas maaga ni A. Clairaut (1754), at L. Euler (1777) ay dumating sa kanila gamit ang termino-by-term na pagsasama. T. r. (1), ang mga coefficient nito ay tinutukoy ng mga formula (2), na tinatawag na. malapit sa Fourier function na f, at ang mga numero a k , b k- Fourier coefficients.
Ang likas na katangian ng mga resulta na nakuha ay depende sa kung paano ang representasyon ng isang function ay nauunawaan bilang isang serye, kung paano ang integral sa mga formula (2) ay naiintindihan. Modernong teorya ng T. ilog. nakuha pagkatapos ng paglitaw ng integral ng Lebesgue.
Ang teorya ng T. r. maaaring may kondisyon na nahahati sa dalawang malalaking seksyon - ang teorya Fourier serye, kung saan ipinapalagay na ang serye (1) ay ang seryeng Fourier ng isang tiyak na tungkulin, at ang teorya ng pangkalahatang T. R., kung saan hindi ginawa ang gayong pagpapalagay. Nasa ibaba ang mga pangunahing resulta na nakuha sa teorya ng pangkalahatang T. r. (sa kasong ito, ang mga set at ang pagsukat ng mga function ay nauunawaan ayon sa Lebesgue).
Ang unang sistematiko pananaliksik T. r., kung saan hindi ipinapalagay na ang mga seryeng ito ay seryeng Fourier, ay ang disertasyon ni V. Riemann (V. Riemann, 1853). Samakatuwid, ang teorya ng pangkalahatang T. r. tinawag minsan ang Riemannian theory ng thermodynamics.
Upang pag-aralan ang mga katangian ng arbitrary na T. r. (1) na may mga coefficient na may posibilidad na zero B. Itinuring ni Riemann ang tuluy-tuloy na function F(x) ,
na ang kabuuan ng isang pare-parehong convergent na serye
nakuha pagkatapos ng dalawang-tiklop na termino-by-term na pagsasama ng serye (1). Kung ang serye (1) ay nagtatagpo sa isang puntong x sa isang numerong s, sa puntong ito ay umiiral ang pangalawang simetriko at katumbas ng s. F function:
pagkatapos ito ay humahantong sa kabuuan ng serye (1) na nabuo ng mga kadahilanan 
tinawag sa pamamagitan ng paraan ng pagbubuod ng Riemann. Gamit ang function na F, ang prinsipyo ng lokalisasyon ng Riemann ay nabuo, ayon sa kung saan ang pag-uugali ng serye (1) sa puntong x ay nakasalalay lamang sa pag-uugali ng function na F sa isang arbitraryong maliit na kapitbahayan ng puntong ito.
Kung si T. r. nagtatagpo sa isang hanay ng positibong sukat, pagkatapos ay ang mga coefficient nito ay malamang na zero (Cantor-Lebesgue). Pagkahilig sa zero coefficients T. r. sumusunod din mula sa tagpo nito sa isang set ng pangalawang kategorya (W. Young, W. Young, 1909).
Isa sa mga pangunahing problema ng teorya ng pangkalahatang thermodynamics ay ang problema ng kumakatawan sa isang arbitrary function T. r. Ang pagpapalakas ng mga resulta ng N. N. Luzin (1915) sa representasyon ng T. R. function sa pamamagitan ng Abel-Poisson at Riemann summable method, pinatunayan ng D. E. Men'shov (1940) ang sumusunod na theorem, na tumutukoy sa pinakamahalagang kaso kapag ang representasyon ng function f ay nauunawaan bilang T. r. sa f(x) halos lahat ng dako. Para sa bawat masusukat at may hangganan na halos lahat ng dako ng function f, mayroong isang T. R. na nagtatagpo dito halos lahat ng dako (Men'shov's theorem). Dapat pansinin na kahit na ang f ay pinagsama-sama, kung gayon, sa pangkalahatan, hindi maaaring kunin ng isa ang seryeng Fourier ng function na f bilang isang serye, dahil may mga seryeng Fourier na naghihiwalay sa lahat ng dako.
Ang teorem ng Men'shov sa itaas ay umamin sa sumusunod na pagpipino: kung ang isang function f ay nasusukat at may hangganan halos lahat ng dako, kung gayon mayroong ganoong 
halos lahat ng dako at ang term-by-term differentiated Fourier series ng function j ay nagtatagpo sa f(x) halos lahat ng dako (N. K. Bari, 1952).
Hindi alam (1984) kung posible bang tanggalin ang kondisyon ng finiteness para sa function f halos lahat ng dako sa Men'shov's theorem. Sa partikular, hindi alam (1984) kung ang T. r. nagtatagpo halos lahat ng dako
Samakatuwid, ang problema ng kumakatawan sa mga pag-andar na maaaring tumagal ng walang katapusang mga halaga sa isang hanay ng positibong panukala ay isinasaalang-alang para sa kaso kapag ito ay pinalitan ng mas mahina na kinakailangan - . Ang convergence sa sukat sa mga function na maaaring tumagal ng walang katapusan na mga halaga ay tinukoy bilang mga sumusunod: bahagyang mga kabuuan ng T. p. s n(x) nagtatagpo sa sukat sa function na f(x) .
kung saan f n(x) nagtatagpo sa / (x) halos lahat ng dako, at ang sequence ay nagtatagpo sa zero sa sukat. Sa setting na ito, ang problema ng representasyon ng mga function ay nalutas hanggang sa wakas: para sa bawat masusukat na function, mayroong isang T. R. na converges dito sa sukat (D. E. Men'shov, 1948).
Maraming pananaliksik ang nakatuon sa problema ng pagiging natatangi ng T. r.: Maaari bang maghiwalay ang dalawang magkaibang T. sa iisang tungkulin? sa ibang pormulasyon: kung T. r. converges sa zero, ito ay sumusunod na ang lahat ng mga coefficients ng serye ay katumbas ng zero. Dito ang isa ay maaaring mangahulugan ng convergence sa lahat ng mga punto o sa lahat ng mga punto sa labas ng isang tiyak na hanay. Ang sagot sa mga tanong na ito ay mahalagang nakadepende sa mga katangian ng set sa labas kung saan hindi ipinapalagay ang convergence.
Ang mga sumusunod na terminolohiya ay naitatag. Maraming pangalan. set ng uniqueness o U- itakda kung, mula sa tagpo ng T. r. sa zero sa lahat ng dako, maliban, marahil, para sa mga punto ng set E, sumusunod na ang lahat ng mga coefficient ng seryeng ito ay katumbas ng zero. Kung hindi Enaz. M-set.
Tulad ng ipinakita ni G. Cantor (1872), pati na rin ang anumang may hangganan ay mga U-set. Ang arbitrary ay isa ring U-set (W. Jung, 1909). Sa kabilang banda, ang bawat hanay ng positibong sukat ay isang M-set.
Ang pagkakaroon ng M-sets of measure ay itinatag ni D. E. Men'shov (1916), na nagtayo ng unang halimbawa ng isang perpektong set na may mga katangiang ito. Ang resultang ito ay may pangunahing kahalagahan sa problema ng pagiging natatangi. Ito ay sumusunod mula sa pagkakaroon ng mga M-set ng sukat na zero na, sa representasyon ng mga pag-andar ng T. R. na nagtatagpo halos lahat ng dako, ang mga seryeng ito ay binibigyang kahulugan nang walang paltos.
Ang perpektong set ay maaari ding maging U-set (N. K. Bari; A. Rajchman, A. Rajchman, 1921). Ang napaka banayad na katangian ng mga hanay ng sukat na zero ay gumaganap ng isang mahalagang papel sa problema ng pagiging natatangi. Ang pangkalahatang tanong tungkol sa pag-uuri ng mga hanay ng sukat na zero sa M- at ang mga U-set ay nananatiling bukas (1984). Hindi ito malulutas kahit para sa mga perpektong set.
Ang sumusunod na problema ay nauugnay sa problema sa pagiging natatangi. Kung si T. r. converges sa function 
kung ang seryeng ito ay dapat na ang seryeng Fourier ng function na /. Si P. Dubois-Reymond (P. Du Bois-Reymond, 1877) ay nagbigay ng positibong sagot sa tanong na ito kung ang f ay pinagsama sa kahulugan ng Riemann at ang serye ay nagtatagpo sa f(x) sa lahat ng mga punto. Mula sa mga resulta III. Ang J. Vallee Poussin (Ch. J. La Vallee Poussin, 1912) ay nagpapahiwatig na ang sagot ay positibo kahit na ang serye ay nagtatagpo sa lahat ng dako maliban sa isang mabibilang na hanay ng mga puntos at ang kabuuan nito ay may hangganan.
Kung ang isang T. p ay ganap na nagtatagpo sa isang punto x 0, kung gayon ang mga punto ng convergence ng seryeng ito, pati na rin ang mga punto ng ganap na tagpo nito, ay matatagpuan sa simetriko na may kinalaman sa puntong x 0
(P. Fatou, P. Fatou, 1906).
Ayon kay Denjoy - Luzin theorem mula sa ganap na tagpo ng T. r. (1) sa isang set ng positibong sukat, ang serye ay nagtatagpo 
at, dahil dito, ang ganap na tagpo ng serye (1) para sa lahat X. Ang ari-arian na ito ay taglay din ng mga hanay ng pangalawang kategorya, gayundin ng ilang partikular na hanay ng sukat na zero.
Sinasaklaw ng survey na ito ang one-dimensional na T. r. (isa). May mga hiwalay na resulta na nauugnay sa pangkalahatang T. p. mula sa ilang mga variable. Dito sa maraming mga kaso kinakailangan pa ring maghanap ng mga natural na pahayag ng problema.
Lit.: Bari N. K., Trigonometric series, M., 1961; Sigmund A., Trigonometric series, trans. mula sa English, tomo 1-2, M., 1965; Luzin N. N., Integral at trigonometric series, M.-L., 1951; Riemann B., Works, trans. mula sa German, M.-L., 1948, p. 225-61.
S. A. Teleyakovsky.
Ensiklopedya sa matematika. - M.: Soviet Encyclopedia. I. M. Vinogradov. 1977-1985.
Alalahanin na sa totoong pagsusuri ang isang trigonometriko na serye ay isang serye sa mga cosine at sine ng maramihang mga arko, i.e. hilera ng form
Medyo kasaysayan. Ang unang panahon ng teorya ng naturang serye ay iniuugnay sa kalagitnaan ng ika-18 siglo na may kaugnayan sa problema ng mga vibrations ng string, nang ang nais na function ay hinanap bilang kabuuan ng serye (14.1). Ang tanong ng posibilidad ng naturang representasyon ay nagdulot ng mainit na debate sa mga mathematician, na tumagal ng ilang dekada. Mga pagtatalo na may kaugnayan sa nilalaman ng konsepto ng function. Sa oras na iyon, ang mga function ay karaniwang nauugnay sa kanilang analytical assignment, ngunit dito ito ay naging kinakailangan upang kumatawan sa isang function sa tabi ng (14.1), na ang graph ay isang medyo arbitrary na curve. Ngunit ang kahalagahan ng mga pagtatalo na ito ay mas malaki. Sa katunayan, nagtaas sila ng mga tanong na may kaugnayan sa maraming pangunahing mahahalagang ideya ng pagsusuri sa matematika.
At sa hinaharap, tulad ng sa unang panahon na ito, ang teorya ng trigonometriko serye ay nagsilbing isang mapagkukunan ng mga bagong ideya. Ito ay may kaugnayan sa kanila, halimbawa, na ang teorya ng set at ang teorya ng mga pag-andar ng isang tunay na variable ay lumitaw.
Sa pangwakas na kabanatang ito, isasaalang-alang natin ang materyal na muling nag-uugnay sa tunay at kumplikadong pagsusuri, ngunit hindi gaanong makikita sa mga aklat-aralin sa TFCT. Sa kurso ng pagsusuri, nagpatuloy sila mula sa isang paunang natukoy na function at pinalawak ito sa isang trigonometric Fourier series. Dito natin isinasaalang-alang ang kabaligtaran na problema: para sa isang naibigay na serye ng trigonometriko, itatag ang tagpo at kabuuan nito. Para dito, matagumpay na ginamit nina Euler at Lagrange ang mga analytic function. Tila, si Euler sa unang pagkakataon (1744) ay nakakuha ng mga pagkakapantay-pantay
Sa ibaba ay sinusunod namin ang mga yapak ni Euler, nililimitahan ang aming sarili lamang sa mga espesyal na kaso ng serye (14.1), ibig sabihin, trigonometric series
Magkomento. Ang sumusunod na katotohanan ay mahalagang gagamitin: kung ang pagkakasunod-sunod ng mga positibong coefficient isang p monotonically ay nagiging zero, pagkatapos ang mga seryeng ito ay magkakaugnay sa anumang saradong agwat na walang mga punto ng form 2lx (hanggang gZ). Sa partikular, sa pagitan (0.2n -) magkakaroon ng pointwise convergence. Tingnan ang tungkol dito sa trabaho, pp. 429-430.
Ang ideya ni Euler sa pagbubuod ng serye (14.4), (14.5) ay iyon, gamit ang pagpapalit z = e a pumunta sa power series
Kung sa loob ng bilog ng yunit ay malinaw na mahahanap ang kabuuan nito, kung gayon ang problema ay kadalasang nalulutas sa pamamagitan ng paghihiwalay ng tunay at haka-haka na mga bahagi mula dito. Binibigyang-diin namin na, gamit ang Euler method, dapat suriin ng isa ang convergence ng serye (14.4), (14.5).
Tingnan natin ang ilang halimbawa. Sa maraming mga kaso, ang geometric na serye ay magiging kapaki-pakinabang
pati na rin ang seryeng nakuha mula rito sa pamamagitan ng term-by-term differentiation o integration. Halimbawa,
Halimbawa 14.1. Hanapin ang kabuuan ng isang serye
Solusyon. Ipinakilala namin ang isang katulad na serye na may mga cosine
Ang parehong serye ay nagtatagpo sa lahat ng dako, dahil majorized ng geometric na serye 1 + r + r 2+.... Ipagpalagay z = e"x, nakukuha namin
Dito ang fraction ay nabawasan sa anyo
kung saan natin makukuha ang sagot sa tanong ng problema:
Sa daan, itinatag namin ang pagkakapantay-pantay (14.2): Halimbawa 14.2. Sumo ng mga hilera
Solusyon. Ayon sa pangungusap sa itaas, ang parehong serye ay nagtatagpo sa tinukoy na agwat at nagsisilbing serye ng Fourier para sa mga function na kanilang tinukoy f(x) 9 g(x). Ano ang mga function na ito? Upang masagot ang tanong, alinsunod sa pamamaraan ng Euler, binubuo namin ang serye (14.6) na may mga coefficient isang p= -. Sumang-ayon-
ngunit pagkakapantay-pantay (14.7) nakukuha natin
Inaalis ang mga detalye (dapat kopyahin ng mambabasa ang mga ito), itinuturo namin na ang expression sa ilalim ng logarithm sign ay maaaring katawanin bilang
Ang modulus ng expression na ito ay katumbas ng -, at ang argumento (mas tiyak, ang pangunahing halaga nito ay
- 2 kasalanan-
halaga) ay pantay Samakatuwid Sa ^ = -ln(2sin
Halimbawa 14.3. Sa -l sum ng mga hilera
Solusyon. Ang parehong serye ay nagtatagpo sa lahat ng dako, dahil sila ay pinangungunahan ng convergent
sa tabi ng karaniwang miyembro -! . Hilera (14.6)
n(n +1)
direkta
J_ _\_ __1_
/?(/? +1) P /1 + 1
ns ay magbibigay ng kilalang halaga. Sa batayan, kinakatawan namin ito sa anyo
pagkakapantay-pantay
Dito ang expression sa panaklong ay ln(l + z) at ang expression sa square bracket ay ^^ + ** ^--. Dahil dito,
= (1 + -)ln(1 + z). Ngayon dapat ilagay dito z = eLX at gawin ang parehong mga hakbang tulad ng sa nakaraang halimbawa. Inaalis ang mga detalye, itinuturo namin iyon Ito ay nananatiling buksan ang mga bracket at isulat ang sagot. Iniiwan namin ito sa mambabasa. Mga gawain para sa kabanata 14 Kalkulahin ang mga kabuuan ng mga sumusunod na hanay. 3.1.a). Kung w=u + iv, pagkatapos at= -r- -v = -^-^ Kaya naman l: 2 + (1-.g) 2 .t 2 + (1-d:) 2 Ang pinagmulan ng mga coordinate ay dapat na hindi kasama sa bilog na ito, dahil (m, v) 9* (0; 0) V* e R, tono at= lim v = 0. x-yx>.v->oo a = 1, a = 2. z "=-! + -> z,=-l - sila w = 2x; ay wala kahit saan holomorphic; St St depende sa variable na "t. Ang mga kundisyon ng Cauchy-Riemann ay nagpapahiwatig na ang mga function na ito ay independiyente rin sa y. 4.5. Isaalang-alang, halimbawa, ang kaso Re f(z) = i(x, y) = const. MULA SA gamit ang mga kundisyon ng Cauchy-Riemann, hulaan mula rito na Im/(z) = v(x 9 y) = const. ang argumento ng derivative ay katumbas ng zero, pagkatapos ang haka-haka na bahagi nito ay zero, at ang tunay na bahagi ay positibo. Mula dito nakukuha ang sagot: tuwid sa = -X-1 (X * 0). b) bilog z + i=j2. ang expression sa panaklong ay nagkaroon ng parehong kahulugan, pagkatapos ay magkakaroon sila na salungat sa irrationality a . sa= 0, -1 x 1 mayroon kami at =--e [-1,1]" v = 0. Isaalang-alang ang pangalawang bahagi ng hangganan - ang kalahating bilog z=e u,tg. Sa seksyong ito, ang expression ay na-convert sa form w=u=-- ,/* -. Sa gitna. Ayon sa (8.6), ang nais na integral ay katumbas ng
b). Ang lower semicircle equation ay may anyo z(t) = e“,t e[l, 2n). Sa pamamagitan ng formula (8.8), ang integral ay katumbas ng z = t + i,te. Sagot: - + - i. .1 .t+2/r e 2 ,e 2. Ito ay sumusunod mula sa mga kondisyon ng problema na pinag-uusapan natin ang pangunahing halaga ng ugat: Vz, i.e. tungkol sa una sa mga ito. Kung gayon ang integral ay 8.3. Sa paglutas ng problema, ang pagguhit ay sadyang hindi ibinigay, ngunit dapat itong kumpletuhin ng mambabasa. Ginagamit ang equation ng isang straight line segment, na nagkokonekta sa dalawang ibinigay na puntos i, /> e C (a - Magsimula, b - dulo): z = (l - /)fl+ /?,/€ . Hatiin natin sa apat ang gustong integral: I = I AB + I BC + I CD +1
D.A. Sa segment AB meron kami z- (1 -1)
? 1 +1
/, kaya ang integral sa segment na ito, ayon sa (8.8), ay katumbas ng Nagpapatuloy sa katulad na paraan, nakita namin area D na naglalaman ng Г at ns na naglalaman a. Sa pamamagitan ng integral theorem na inilapat sa /),/], ang nais na integral ay katumbas ng zero. geometric na serye 1 + q + q2 (|| kumakatawan sa anyong /(z) = /(-^z). Nang walang pagkawala ng pangkalahatan, maaari nating ipagpalagay iyon ang radius ng convergence ng Taylor series ng function na nakasentro sa point 0 ay mas malaki sa isa. Meron kami: Ang mga halaga ng function ay pareho sa isang discrete set na may limitasyon na punto na kabilang sa bilog ng convergence. Sa pamamagitan ng uniqueness theorem /(z) = const. 11.3. Ipagpalagay natin na ang gustong analytic function na /(z) ay umiiral. Ihambing natin ang mga halaga nito sa pag-andar (z) = z2 sa set E, binubuo ng mga tuldok z n = - (n = 2,3,...). Ang kanilang mga kahulugan ay pareho, at mula noon E ay may limitasyong punto na kabilang sa ibinigay na bilog, pagkatapos ay sa pamamagitan ng uniqueness theorem /(z) = z 2 para sa lahat ng argumento ng ibinigay na bilog. Ngunit ito ay sumasalungat sa kondisyon /(1) = 0. Sagot: ns ay hindi umiiral. 12.2. a). Kinakatawan ang function sa form at palawakin ang mga panaklong. simpleng poste 1,-1,/. Ang kabuuan ng mga nalalabi sa mga ito ay katumbas ng --, at ang integral ay katumbas ng sa). Kabilang sa mga poste 2 Trki(kGZ) ng integrand, dalawa lang ang nasa loob ng ibinigay na bilog. Ito ay 0 at 2 ako pareho silang simple, ang mga nalalabi sa mga ito ay pantay sa 1. Sagot: 4z7. i-multiply ito sa 2/r/. Inaalis ang mga detalye, ipinapahiwatig namin ang sagot: / = -i . 13.2. a). Ilagay natin ang e"=z, pagkatapos e"idt =dz
, dt= - .
Ho e" - e~" z-z~ x kasalanan / =-=-, ang intefal ay mababawasan sa anyo Dito ang denominator ay factorized (z-z,)(z-z 2), kung saan ang z, = 3 - 2 V2 / ay nasa loob ng bilog sa
, a z,=3 + 2V2 / lies sa itaas. Ito ay nananatili upang mahanap ang nalalabi na may paggalang sa simpleng poste z, gamit ang formula (13.2) at b) . Ipagpalagay, tulad ng nasa itaas, e" = z
, binabawasan namin ang intefal sa anyo Ang subintephal function ay may tatlong simpleng pole (alin?). Iniwan ang mambabasa upang kalkulahin ang mga nalalabi sa kanila, ipinapahiwatig namin ang sagot: ako=
. katumbas ng 2(^-1- h-dt).
Tukuyin ang integral sa mga bracket sa pamamagitan ng /. Ang paglalapat ng pagkakapantay-pantay cos "/ = - (1 + cos2f) makuha natin iyon / = [- cit
. Sa pamamagitan ng pagkakatulad sa mga kaso a), b) gumawa ng isang pagpapalit e 2,t
= z, bawasan ang integral sa anyo kung saan ang integration curve ay ang parehong unit circle. Ang mga karagdagang argumento ay pareho sa kaso a). Sagot: ang orihinal, hinahangad na integral ay katumbas ng /r(2-n/2). 13.3. a). Isaalang-alang ang auxiliary complex integral /(/?)= f f(z)dz, saan f(z) = - p-, G (I) - isang tabas na binubuo ng kalahating bilog y(R): | z |= R> 1, Imz > 0 at lahat ng diameters (gumawa ng drawing). Hatiin natin ang integral na ito sa dalawang bahagi - ayon sa pagitan [-/?,/?] at ayon sa y(R). sa. Oo. Mga simpleng pole lamang ang nakahiga sa loob ng circuit z 0 \u003d e 4, z, = e 4 (Larawan 186). Nalaman namin na may paggalang sa kanilang mga nalalabi: Ito ay nananatiling upang i-verify na ang integral tapos na y(R) may posibilidad na zero bilang R. Mula sa hindi pagkakapantay-pantay |g + A|>||i|-|/>|| at mula sa pagtatantya ng integral para sa z e y(R) sinusundan nito iyon
Mga karaniwang pamamaraan, ngunit umabot sa isang patay na dulo sa isa pang halimbawa.
Ano ang hirap at saan maaaring magkaroon ng sagabal? Isantabi natin ang sabon na lubid, mahinahong pag-aralan ang mga dahilan at kilalanin ang mga praktikal na paraan ng solusyon.
Una at pinakamahalaga: sa karamihan ng mga kaso, upang pag-aralan ang convergence ng isang serye, kinakailangan na mag-aplay ng ilang pamilyar na pamamaraan, ngunit ang karaniwang termino ng serye ay puno ng nakakalito na pagpupuno na hindi malinaw kung ano ang gagawin dito. . At lumibot ka sa mga bilog: ang unang tanda ay hindi gumagana, ang pangalawa ay hindi gumagana, ang pangatlo, ikaapat, ikalimang paraan ay hindi gumagana, pagkatapos ay ang mga draft ay itinapon sa isang tabi at ang lahat ay nagsisimula muli. Ito ay kadalasang dahil sa kakulangan ng karanasan o mga puwang sa ibang mga seksyon ng calculus. Sa partikular, kung tumatakbo mga limitasyon ng pagkakasunud-sunod at mababaw na disassembled mga limitasyon sa pag-andar, pagkatapos ay magiging mahirap.
Sa madaling salita, hindi nakikita ng isang tao ang kinakailangang solusyon dahil sa kakulangan ng kaalaman o karanasan.
Minsan ang "eclipse" ay dapat ding sisihin, kapag, halimbawa, ang kinakailangang pamantayan para sa convergence ng serye ay hindi natupad, ngunit dahil sa kamangmangan, hindi pansin o kapabayaan, ito ay nahuhulog sa paningin. At parang sa bike na iyon kung saan nalutas ng propesor ng matematika ang isang problema ng mga bata sa tulong ng mga ligaw na paulit-ulit na pagkakasunud-sunod at serye ng numero =)
Sa pinakamahusay na mga tradisyon, agad na buhay na mga halimbawa: mga hilera 
at ang kanilang mga kamag-anak - magkakaiba, dahil sa teorya ito ay pinatunayan mga limitasyon ng pagkakasunud-sunod. Malamang, sa unang semestre ay matatalo ka sa iyong kaluluwa para sa isang patunay ng 1-2-3 na pahina, ngunit sa ngayon ay sapat na upang ipakita na ang kinakailangang kondisyon para sa convergence ng serye ay hindi natutugunan, na tumutukoy sa mga kilalang katotohanan. sikat? Kung ang mag-aaral ay hindi alam na ang ugat ng nth degree ay isang napakalakas na bagay, kung gayon, sabihin nating, ang serye 
ilagay siya sa isang gulo. Bagaman ang solusyon ay parang dalawa at dalawa: , i.e. para sa malinaw na mga kadahilanan, ang parehong serye ay naghihiwalay. Ang isang katamtamang komento na "ang mga limitasyong ito ay napatunayan sa teorya" (o kahit na ang kawalan nito sa lahat) ay sapat na para sa offset, pagkatapos ng lahat, ang mga kalkulasyon ay medyo mabigat at tiyak na hindi sila kabilang sa seksyon ng mga serye ng numero.
At pagkatapos pag-aralan ang mga susunod na halimbawa, magugulat ka lang sa kaiklian at transparency ng maraming solusyon:
Halimbawa 1
Siyasatin ang convergence ng isang serye
Solusyon: una sa lahat, suriin ang pagpapatupad kinakailangang criterion para sa convergence. Ito ay hindi isang pormalidad, ngunit isang magandang pagkakataon upang harapin ang halimbawa ng "maliit na pagdanak ng dugo".
Ang "Inspeksyon ng eksena" ay nagmumungkahi ng isang magkakaibang serye (ang kaso ng isang pangkalahatang maharmonya na serye), ngunit muli ang tanong ay lumitaw, kung paano isaalang-alang ang logarithm sa numerator?
Tinatayang mga halimbawa ng mga gawain sa pagtatapos ng aralin.
Karaniwan kapag kailangan mong magsagawa ng dalawang-daan (o kahit tatlong-daan) na pangangatwiran:
Halimbawa 6
Siyasatin ang convergence ng isang serye 
Solusyon: una, maingat na harapin ang kalokohan ng numerator. Limitado ang pagkakasunod-sunod: . Pagkatapos: 
Ihambing natin ang ating serye sa serye. Sa bisa ng dobleng hindi pagkakapantay-pantay na nakuha, para sa lahat ng "en" ito ay magiging totoo: 
Ngayon, ihambing natin ang serye sa magkakaibang maharmonya na serye.
Fraction denominator mas mababa ang denominator ng fraction, kaya ang fraction mismo – higit pa fractions (isulat ang unang ilang termino, kung hindi malinaw). Kaya, para sa anumang "en": 
Kaya, sa paghahambing, ang serye 
diverges kasama ang harmonic series.
Kung babaguhin natin ng kaunti ang denominator: 
, kung gayon ang unang bahagi ng pangangatwiran ay magiging katulad: 
. Ngunit upang patunayan ang pagkakaiba-iba ng serye, tanging ang limitasyon ng pagsubok ng paghahambing ang naaangkop na, dahil ang hindi pagkakapantay-pantay ay mali.
Ang sitwasyon na may converging series ay "mirror", iyon ay, halimbawa, para sa isang serye, ang parehong pamantayan sa paghahambing ay maaaring gamitin (ang hindi pagkakapantay-pantay ay totoo), at para sa isang serye, tanging ang limitasyong pamantayan (ang hindi pagkakapantay-pantay ay mali).
Ipinagpapatuloy namin ang aming safari sa kagubatan, kung saan ang isang kawan ng mga magaganda at makatas na antelope ay nakaharap sa abot-tanaw:
Halimbawa 7
Siyasatin ang convergence ng isang serye
Solusyon: ang kinakailangang convergence criterion ay nasiyahan, at muli naming itanong ang klasikong tanong: ano ang gagawin? Bago sa amin ay isang bagay na kahawig ng isang convergent na serye, gayunpaman, walang malinaw na panuntunan dito - ang gayong mga asosasyon ay kadalasang mapanlinlang.
Madalas, ngunit hindi sa pagkakataong ito. Sa pamamagitan ng paggamit Limitahan ang paghahambing na pamantayan Ihambing natin ang ating serye sa convergent series . Kapag kinakalkula ang limitasyon, ginagamit namin kahanga-hangang limitasyon 
, kung saan bilang infinitesimal nakatayo: 
nagtatagpo kasama ang katabi .
Sa halip na gamitin ang karaniwang artipisyal na pamamaraan ng pagpaparami at paghahati sa pamamagitan ng isang "tatlo", posible na unang ihambing sa isang convergent na serye.
Ngunit narito ang isang caveat ay kanais-nais na ang constant-multiplier ng pangkalahatang termino ay hindi nakakaapekto sa tagpo ng serye. At sa ganitong istilo lamang ang solusyon ng sumusunod na halimbawa ay idinisenyo:
Halimbawa 8
Siyasatin ang convergence ng isang serye
Halimbawa sa katapusan ng aralin.
Halimbawa 9
Siyasatin ang convergence ng isang serye
Solusyon: sa mga nakaraang halimbawa, ginamit namin ang boundedness ng sine, ngunit ngayon ang pag-aari na ito ay wala sa play. Ang denominator ng isang fraction ng mas mataas pagkakasunud-sunod ng paglago kaysa sa numerator, kaya kapag ang argument ng sine at ang buong karaniwang termino walang katapusang maliit. Ang kinakailangang kondisyon para sa convergence, tulad ng naiintindihan mo, ay nasiyahan, na hindi nagpapahintulot sa amin na umiwas sa trabaho.
Magsasagawa kami ng reconnaissance: alinsunod sa kapansin-pansing pagkakapareho 
, itapon sa isip ang sine at kumuha ng serye. Well, isang bagay na tulad nito….
Paggawa ng desisyon:
Ihambing natin ang seryeng pinag-aaralan sa magkakaibang serye. Ginagamit namin ang pamantayan sa paghahambing ng limitasyon: 
Palitan natin ang infinitesimal ng katumbas: para 
.
Ang isang may hangganang numero maliban sa zero ay nakuha, na nangangahulugan na ang seryeng pinag-aaralan diverges kasama ang harmonic series.
Halimbawa 10
Siyasatin ang convergence ng isang serye
Ito ay isang halimbawa ng do-it-yourself.
Para sa pagpaplano ng karagdagang mga aksyon sa mga naturang halimbawa, ang mental na pagtanggi ng sine, arcsine, tangent, arctangent ay nakakatulong nang malaki. Ngunit tandaan, ang posibilidad na ito ay umiiral lamang kapag infinitesimal argumento, hindi pa katagal nakatagpo ako ng isang mapanuksong serye:
Halimbawa 11
Siyasatin ang convergence ng isang serye 
.
Solusyon: walang silbi na gamitin ang limitasyon ng arc tangent dito, at hindi rin gumagana ang equivalence. Ang output ay nakakagulat na simple: 
Serye ng Pag-aaral diverges, dahil hindi nasiyahan ang kinakailangang criterion para sa convergence ng serye.
Ang pangalawang dahilan Ang "Gag on the job" ay binubuo ng isang disenteng pagiging sopistikado ng karaniwang miyembro, na nagiging sanhi ng mga paghihirap na teknikal. Sa halos pagsasalita, kung ang seryeng tinalakay sa itaas ay nabibilang sa kategorya ng "mga figure na hulaan mo", kung gayon ang mga ito ay nabibilang sa kategorya ng "magpasya ka". Sa totoo lang, ito ay tinatawag na pagiging kumplikado sa "karaniwan" na kahulugan. Hindi lahat ay maayos na malulutas ang ilang mga factorial, degree, ugat at iba pang mga naninirahan sa savannah. Siyempre, ang mga factorial ay nagdudulot ng pinakamaraming problema:
Halimbawa 12
Siyasatin ang convergence ng isang serye
Paano itaas ang isang factorial sa isang kapangyarihan? Madali. Ayon sa panuntunan ng mga operasyon na may mga kapangyarihan, kinakailangang itaas ang bawat kadahilanan ng produkto sa isang kapangyarihan:
At, siyempre, pansin at muli pansin, ang d'Alembert sign mismo ay gumagana nang tradisyonal: 
Kaya, ang seryeng pinag-aaralan nagtatagpo.
Ipinaaalala ko sa iyo ang isang makatwirang pamamaraan para sa pag-aalis ng kawalan ng katiyakan: kapag ito ay malinaw pagkakasunud-sunod ng paglago numerator at denominator - hindi na kailangang magdusa at buksan ang mga bracket.
Halimbawa 13
Siyasatin ang convergence ng isang serye
Ang hayop ay napakabihirang, ngunit ito ay natagpuan, at ito ay magiging hindi patas na laktawan ito gamit ang isang lens ng camera.
Ano ang double exclamation point factorial? Ang factorial "wind" ang produkto ng mga positibong even na numero: 
Katulad nito, ang factorial ay "wind up" ang produkto ng mga positibong kakaibang numero: 
Suriin kung ano ang pagkakaiba sa pagitan
Halimbawa 14
Siyasatin ang convergence ng isang serye
At sa gawaing ito, subukang huwag malito sa mga degree, kahanga-hangang pagkakapareho at kahanga-hangang mga limitasyon.
Mga halimbawang solusyon at sagot sa pagtatapos ng aralin.
Ngunit ang mag-aaral ay nakakakain hindi lamang ng mga tigre - ang mga tusong leopardo ay sumusubaybay din sa kanilang biktima:
Halimbawa 15
Siyasatin ang convergence ng isang serye 
Solusyon: ang kinakailangang criterion ng convergence, ang limiting criterion, ang d'Alembert at Cauchy na pamantayan ay nawawala halos kaagad. Ngunit ang pinakamasama sa lahat, ang tampok na may mga hindi pagkakapantay-pantay, na paulit-ulit na nagligtas sa atin, ay walang kapangyarihan. Sa katunayan, ang paghahambing sa isang magkakaibang serye ay imposible, dahil ang hindi pagkakapantay-pantay 
hindi tama - pinapataas lang ng multiplier-logarithm ang denominator, binabawasan ang mismong fraction 
kaugnay ng fraction. At isa pang pandaigdigang tanong: bakit kami sa simula ay sigurado na ang aming serye 
ay nakasalalay sa diverge at dapat ihambing sa ilang magkakaibang serye? Nababagay ba siya sa lahat?
Integral na tampok? Hindi wastong integral 
nagdudulot ng malungkot na kalooban. Ngayon, kung mayroon kaming isang hilera 
… tapos oo. Tumigil ka! Ito ay kung paano ipinanganak ang mga ideya. Gumagawa kami ng desisyon sa dalawang hakbang:
1) Una, pinag-aaralan natin ang convergence ng serye 
. Ginagamit namin mahalagang katangian:
Integrand tuloy-tuloy sa
Kaya, isang numero 
nag-iiba kasama ang kaukulang di-wastong integral.
2) Ihambing ang aming serye sa magkakaibang serye 
. Ginagamit namin ang pamantayan sa paghahambing ng limitasyon:
Ang isang may hangganang numero maliban sa zero ay nakuha, na nangangahulugan na ang seryeng pinag-aaralan diverges kasama ang magkatabi 
.
At walang hindi pangkaraniwan o malikhain sa naturang desisyon - ganyan dapat magpasya!
Iminumungkahi kong independiyenteng iguhit ang sumusunod na dalawang hakbang:
Halimbawa 16
Siyasatin ang convergence ng isang serye 
Ang isang mag-aaral na may ilang karanasan sa karamihan ng mga kaso ay agad na nakikita kung ang serye ay nagtatagpo o nag-iiba, ngunit nangyayari na ang isang mandaragit ay matalinong nagkukunwari sa mga palumpong:
Halimbawa 17
Siyasatin ang convergence ng isang serye 
Solusyon: sa unang tingin, hindi talaga malinaw kung paano kumilos ang seryeng ito. At kung mayroon tayong fog sa harap natin, lohikal na magsimula sa isang magaspang na pagsusuri ng kinakailangang kondisyon para sa convergence ng serye. Upang maalis ang kawalan ng katiyakan, gumagamit kami ng isang hindi nalulubog paraan ng multiplikasyon at paghahati sa pamamagitan ng magkadugtong na pagpapahayag:
Ang kinakailangang tanda ng convergence ay hindi gumana, ngunit dinala ang aming kasamang Tambov sa liwanag. Bilang resulta ng mga ginawang pagbabago, nakuha ang isang katumbas na serye 
, na kung saan ay malakas na kahawig ng isang convergent series.
Sumulat kami ng isang malinis na solusyon:
Ihambing ang seryeng ito sa convergent series. Ginagamit namin ang pamantayan sa paghahambing ng limitasyon:
I-multiply at hatiin sa magkadugtong na expression:
Ang isang may hangganang numero maliban sa zero ay nakuha, na nangangahulugan na ang seryeng pinag-aaralan nagtatagpo kasama ang katabi .
Marahil ang ilan ay may tanong, saan nanggaling ang mga lobo sa ating African safari? hindi ko alam. Malamang dinala nila. Makukuha mo ang sumusunod na balat ng tropeo:
Halimbawa 18
Siyasatin ang convergence ng isang serye 
Isang halimbawang solusyon sa pagtatapos ng aralin
At, sa wakas, isa pang pag-iisip na bumibisita sa maraming estudyanteng nasa kawalan ng pag-asa: sa halip na gumamit ng mas bihirang pamantayan para sa convergence ng serye? Tanda ng Raabe, tanda ni Abel, tanda ng Gauss, tanda ng Dirichlet at iba pang hindi kilalang mga hayop. Gumagana ang ideya, ngunit sa mga totoong halimbawa ay napakabihirang ipinatupad. Sa personal, sa lahat ng mga taon ng pagsasanay, mayroon lamang akong 2-3 beses na ginamit tanda ni Raabe kapag wala talagang nakatulong mula sa karaniwang arsenal. Binubuo ko ang kurso ng aking matinding pakikipagsapalaran:
Halimbawa 19
Siyasatin ang convergence ng isang serye
Solusyon: Walang anumang pag-aalinlangan isang tanda ng d'Alembert. Sa kurso ng mga kalkulasyon, aktibong ginagamit ko ang mga katangian ng mga degree, pati na rin pangalawang kahanga-hangang limitasyon:
Narito ang isa para sa iyo. Ang tanda ni D'Alembert ay hindi nagbigay ng sagot, bagama't walang naglalarawan ng gayong kinalabasan.
Matapos dumaan sa manwal, nakakita ako ng isang maliit na kilalang limitasyon na napatunayan sa teorya at naglapat ng mas malakas na radikal na pamantayan ng Cauchy:
Narito ang dalawa para sa iyo. At, higit sa lahat, hindi malinaw kung ang serye ay nagtatagpo o naghihiwalay (isang napakabihirang sitwasyon para sa akin). Kailangang tanda ng paghahambing? Nang walang labis na pag-asa - kahit na sa isang hindi maisip na paraan ay nalaman ko ang pagkakasunud-sunod ng paglaki ng numerator at denominator, hindi pa rin ito ginagarantiyahan ng isang gantimpala.
Isang kumpletong d'Alembert, ngunit ang pinakamasama ay ang serye ay kailangang malutas. Kailangan. Pagkatapos ng lahat, ito ang unang pagkakataon na susuko ako. At pagkatapos ay naalala ko na tila may ilang mas makapangyarihang mga palatandaan. Bago ako ay hindi na isang lobo, hindi isang leopardo at hindi isang tigre. Isa itong malaking elepante na kumakaway sa isang malaking puno. Kinailangan kong kumuha ng grenade launcher:
Tanda ni Raabe
Isaalang-alang ang isang positibong serye ng numero.
Kung may limitasyon 
, pagkatapos:
a) Sa isang hilera diverges. Bukod dito, ang resultang halaga ay maaaring zero o negatibo.
b) Sa isang hilera nagtatagpo. Sa partikular, ang serye ay nagtatagpo para sa .
c) Kailan Walang sagot ang tanda ni Raabe.
Binubuo namin ang limitasyon at maingat na pinasimple ang fraction: 
Oo, ang larawan ay, upang ilagay ito nang mahinahon, hindi kanais-nais, ngunit hindi na ako nagulat. lopital na mga patakaran, at ang unang naisip, tulad ng nangyari sa ibang pagkakataon, ay naging tama. Ngunit una, sa loob ng halos isang oras, pinilipit ko at pinihit ang limitasyon gamit ang "karaniwan" na mga pamamaraan, ngunit ang kawalan ng katiyakan ay hindi nais na maalis. At ang paglalakad sa mga bilog, tulad ng iminumungkahi ng karanasan, ay isang tipikal na palatandaan na ang maling paraan ng paglutas ay napili.
Kinailangan kong bumaling sa karunungan ng katutubong Ruso: "Kung walang makakatulong, basahin ang mga tagubilin." At nang buksan ko ang 2nd volume ng Fichtenholtz, sa aking labis na kagalakan nakakita ako ng isang pag-aaral ng isang magkatulad na serye. At pagkatapos ay napunta ang solusyon ayon sa modelo.
Sa agham at teknolohiya, madalas na kailangang harapin ng isang tao ang mga pana-panahong phenomena, i.e. yaong mga muling ginawa pagkatapos ng isang tiyak na tagal ng panahon T tinatawag na period. Ang pinakasimpleng periodic function (maliban sa isang pare-pareho) ay isang sinusoidal na halaga: tulad ng sa(x+ ), harmonic oscillation, kung saan mayroong "frequency" na nauugnay sa panahon sa pamamagitan ng ratio: . Mula sa gayong simpleng mga pana-panahong pag-andar, ang mga mas kumplikado ay maaaring binubuo. Malinaw, ang mga constituent sinusoidal na dami ay dapat na magkaibang mga frequency, dahil ang pagdaragdag ng mga sinusoidal na dami ng parehong frequency ay nagreresulta sa isang sinusoidal na dami ng parehong frequency. Kung magdagdag kami ng ilang mga halaga ng form
Halimbawa, pinaparami namin dito ang pagdaragdag ng tatlong sinusoidal na dami: . Isaalang-alang ang graph ng function na ito
Malaki ang pagkakaiba ng graph na ito sa isang sine wave. Ito ay higit na totoo para sa kabuuan ng isang walang katapusang serye na binubuo ng mga termino ng ganitong uri. Ibigay natin ang tanong: posible ba ang isang naibigay na periodic function ng period T kumakatawan bilang kabuuan ng isang may hangganan o hindi bababa sa isang walang katapusang hanay ng mga sinusoidal na dami? Ito ay lumalabas na may kinalaman sa isang malaking klase ng mga pag-andar, ang tanong na ito ay masasagot sa sang-ayon, ngunit ito ay kung isasama lamang natin nang tumpak ang buong walang katapusang pagkakasunud-sunod ng mga naturang termino. Sa geometriko, nangangahulugan ito na ang graph ng isang periodic function ay nakuha sa pamamagitan ng pagpapatong ng isang serye ng mga sinusoid. Kung isasaalang-alang natin ang bawat halaga ng sinusoidal bilang isang tiyak na maharmonya na paggalaw ng oscillatory, maaari nating sabihin na ito ay isang kumplikadong oscillation na nailalarawan sa pamamagitan ng isang function o sa pamamagitan lamang ng mga harmonic nito (una, pangalawa, atbp.). Ang proseso ng agnas ng isang pana-panahong pag-andar sa mga harmonika ay tinatawag maharmonya na pagsusuri.
Mahalagang tandaan na ang mga naturang pagpapalawak ay kadalasang nagiging kapaki-pakinabang sa pag-aaral ng mga pag-andar na ibinibigay lamang sa isang tiyak na may hangganang pagitan at hindi nabubuo sa lahat ng anumang oscillatory phenomena.
Kahulugan. Ang isang trigonometric series ay isang serye ng anyo:
O kaya 
(1).
Ang mga tunay na numero ay tinatawag na coefficients ng trigonometric series. Ang seryeng ito ay maaari ding isulat ng ganito:
Kung ang isang serye ng uri na ipinakita sa itaas ay nagtatagpo, kung gayon ang kabuuan nito ay isang periodic function na may period 2p.
Kahulugan. Ang Fourier coefficients ng isang trigonometric series ay tinatawag na: 
(2)
(3)
(4)
Kahulugan. Malapit sa Fourier para sa isang function f(x) ay tinatawag na trigonometric series na ang mga coefficient ay ang Fourier coefficients.
Kung ang Fourier series ng function f(x) converges dito sa lahat ng mga punto ng pagpapatuloy, pagkatapos ay sinasabi namin na ang function f(x) lumalawak sa isang seryeng Fourier.
Teorama.(Dirichlet's theorem) Kung ang isang function ay may panahon na 2p at tuluy-tuloy sa isang segment o may hangganang bilang ng mga discontinuity point ng unang uri, ang segment ay maaaring hatiin sa isang may hangganang bilang ng mga segment upang ang function ay monotoniko sa loob ng bawat isa. ng mga ito, pagkatapos ay ang seryeng Fourier para sa function ay nagtatagpo para sa lahat ng mga halaga X, at sa mga punto ng pagpapatuloy ng function, ang kabuuan nito S(x) ay katumbas ng , at sa mga discontinuity point ang kabuuan nito ay katumbas ng , i.e. ang ibig sabihin ng aritmetika ng mga halaga ng limitasyon sa kaliwa at kanan.
Sa kasong ito, ang Fourier series ng function f(x) pantay na nagtatagpo sa anumang pagitan na kabilang sa pagitan ng pagpapatuloy ng function.
Ang isang function na nakakatugon sa mga kondisyon ng theorem na ito ay tinatawag na piecewise smooth sa pagitan.
Isaalang-alang natin ang mga halimbawa sa pagpapalawak ng isang function sa isang seryeng Fourier.
Halimbawa 1. Palawakin ang function sa isang Fourier series f(x)=1-x, na may period 2p at ibinigay sa segment .
Solusyon. I-plot natin ang function na ito
Ang function na ito ay tuloy-tuloy sa segment , iyon ay, sa isang segment na may haba ng isang tuldok, samakatuwid maaari itong palawakin sa isang seryeng Fourier na nagtatagpo dito sa bawat punto ng segment na ito. Gamit ang formula (2), makikita natin ang coefficient ng seryeng ito: .
Inilapat namin ang formula ng integration-by-parts at hinahanap at ginagamit namin ang mga formula (3) at (4), ayon sa pagkakabanggit:
Ang pagpapalit ng mga coefficient sa formula (1), nakukuha namin 
o .
Ang pagkakapantay-pantay na ito ay nagaganap sa lahat ng mga punto, maliban sa mga punto at (mga gluing point ng mga graph). Sa bawat isa sa mga puntong ito, ang kabuuan ng serye ay katumbas ng arithmetic mean ng mga halaga ng limitasyon nito sa kanan at kaliwa, iyon ay.
Ipakita natin ang isang algorithm para sa pagpapalawak ng function sa isang seryeng Fourier.
Ang pangkalahatang pamamaraan para sa paglutas ng problemang iniharap ay ang mga sumusunod.
